Úloha k procvičení
ÚLOHA 1: Proveďte dekompozici časové řady pozorované při měřeních koncentrace CO2 v ovzduší. Soubor dat, který je dostupný na: http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4411.htm obsahuje měsíční průměrné koncentrace CO2 na observatoři Mauna Loa v letech 1974 – 1987. Koncentrace jsou udávány v bezrozměrných jednotkách, jako molární zlomek (mole fraction).
Tab. 6.1: Ukázka datového souboru pro modelovanou časovou řadu v úloze 1. Soubor obsahuje celkem 161 řádků, kde každý řádek reprezentuje jedno měření průměrné měsíční koncentrace CO2.
| CO2 | Rok a měsíc | Rok | Měsíc |
|---|---|---|---|
| 333.13 | 1974.38 | 1974 | 5 |
| 332.09 | 1974.46 | 1974 | 6 |
| 331.10 | 1974.54 | 1974 | 7 |
| 329.14 | 1974.63 | 1974 | 8 |
| 327.36 | 1974.71 | 1974 | 9 |
| 327.29 | 1974.79 | 1974 | 10 |
| 328.23 | 1974.88 | 1974 | 11 |
| 329.55 | 1974.96 | 1974 | 12 |
| 330.62 | 1975.04 | 1975 | 1 |
| 331.40 | 1975.13 | 1975 | 2 |
| 331.87 | 1975.21 | 1975 | 3 |
| 333.18 | 1975.29 | 1975 | 4 |
| 333.92 | 1975.38 | 1975 | 5 |
Data, která jsou na uvedené adrese k dispozici v textovém formátu, je třeba nejdříve převést běžnými softwarovými prostředky do souboru ve formátu CSV (comma separated values), kde jsou na každém řádku k dispozici všechny numerické hodnoty k jednomu měření oddělené čárkou, tabulátorem nebo středníkem. Každé měření je reprezentováno čtyřmi parametry, z toho tři reprezentují údaje na časové ose, jak ukazuje tab. 6.1.
Kód skriptu, který v Matlabu realizuje načtení dat, jejich vykreslení, analýzu trendu a periodických komponent je na obr. 6.4. Na obr. 6.5 je časová řada vykreslena spolu s vypočítanou lineární trendovou funkcí. Obr. 6.6 ukazuje grafickou analýzu čar v diskrétním spektru vypočteném z časové řady očištěné od lineárního trendu. Výsledkem analýzy jsou dvě významné harmonické komponenty s periodou 12 a 6 měsíců. Sezónní diferencování s periodou 12 vzorků utlumí obě tyto komponenty (i další vyšší harmonické), jak je vysvětleno v textu výukové jednotky Náhodné procesy a modely časových řad - Boxovy a Jenkinsovy modely a na obr. 6.3.
Obr. 6.4: Úloha 1 – modelování časové řady s měsíčními koncentracemi CO2.
První část: dekompozice.
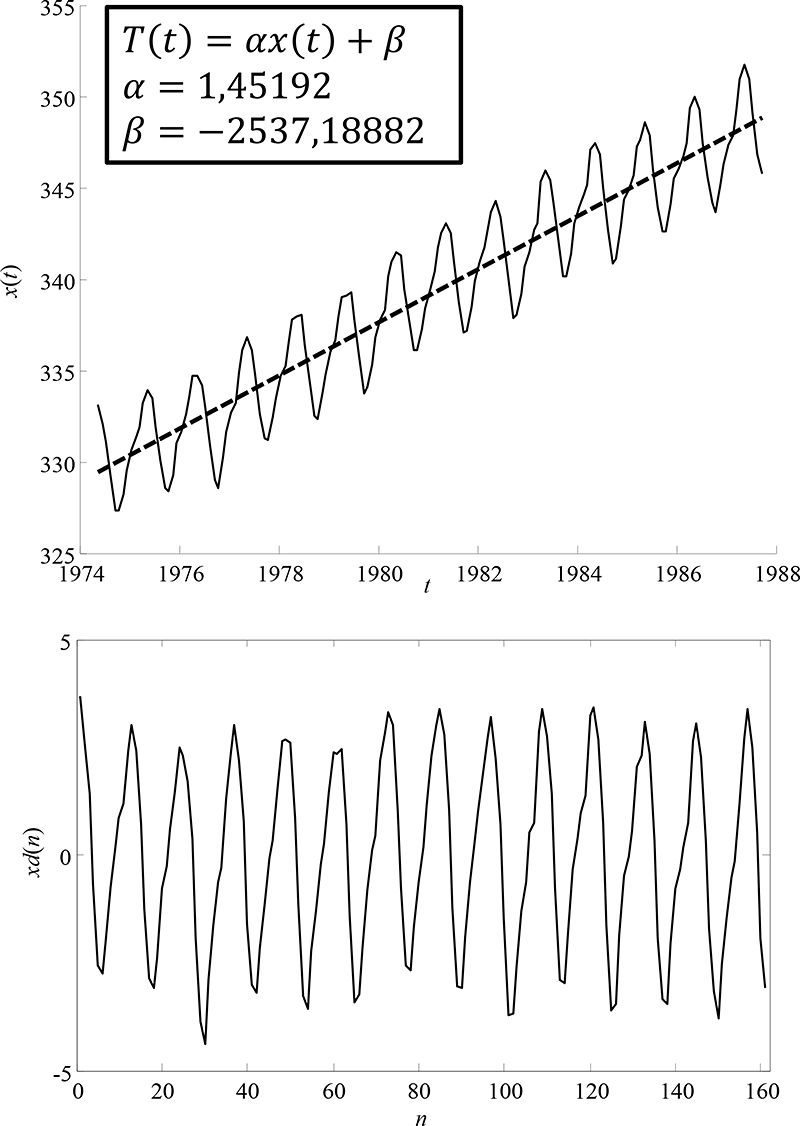
Obr. 6.5: Nahoře: časová řada x(t) s měsíčními koncentracemi CO2 v ovzduší a lineární trendová funkce T(t) vypočítaná z x(t) pomocí metody nejmenších čtverců. Dole: časová řada x(t) očištěná od lineárního trendu a s indexem vzorku n jako nezávisle proměnnou.
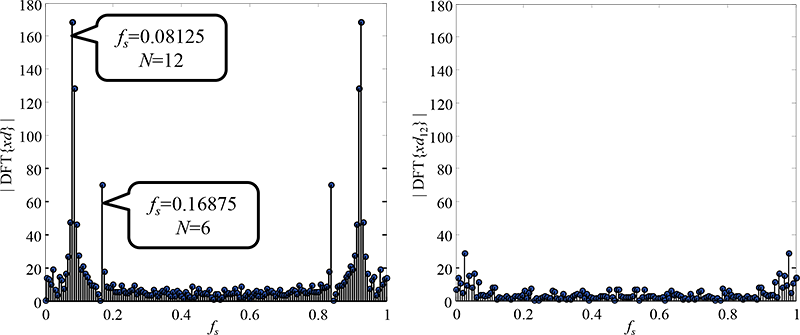
Obr. 6.6: Zjišťování periody významných cyklických/sezónních jevů. Amplitudová část diskrétního spektra: vlevo - časové řady očištěné od lineárního trendu dx(n)=x(n)-T(n), vpravo - časové řady očištěné od lineárního trendu a po sezónním diferencování s periodou 12 vzorků. Při zjišťování periody ve frekvenční doméně je nutno mít na paměti, že spektrum je diskrétní a frekvenční osa je vzorkována podle počtu vzorků časové řady, viz rov. 2.8 pro definici DFT. V časové řadě xd(n) je 161 vzorků a v časové řadě xd12(n) je po sezónním diferencování 149 vzorků.