Pravděpodobnostní funkce

V části Pravděpodobnost a Čebyševova nerovnost bylo ukázáno, že pravděpodobnosti lze považovat za speciální případy časových průměrů. Ze vztahu (6.10) lze odvodit pravděpodobnost, že časová řada x(n) nabude hodnoty mezi X a X+DX, a to pomocí časového průměru obdélníkové funkce s šířkou DX [1]:

Pravděpodobnostní funkce f_x(X) je dána podílem této pravděpodobnosti a šířkou intervalu DX, což při DX blížící se v limitě nule dává:

Plocha pod normalizovanou obdélníkovou funkcí v (6.34) bude jednotková pro jakoukoli šířku intervalu DX. Pro DX blížící se k nule bude tato funkce jednotkovým impulsem d(X). To znamená, že pravděpodobnostní funkci lze formálně zapsat jako časový průměr funkce d [1]:

(6.35)

Pravděpodobnostní funkce f_x(X) vyjadřuje pravděpodobnost, že hodnota časové řady x(n) leží ve velmi úzkém intervalu se středem v x(n)=X, normovanou šířkou tohoto intervalu. Malé písmeno x v f_x(X) reprezentuje náhodnou časovou řadu x(n) a velké písmeno X reprezentuje konkrétní střed intervalu, pro který je pravděpodobnost počítána. Tato dvě písmena tedy spolu přímo nesouvisí. Např. f_y(X)DX vyjadřuje pravděpodobnost, že hodnota časové řady y(n) je v intervalu o šířce DX centrovaném v X.

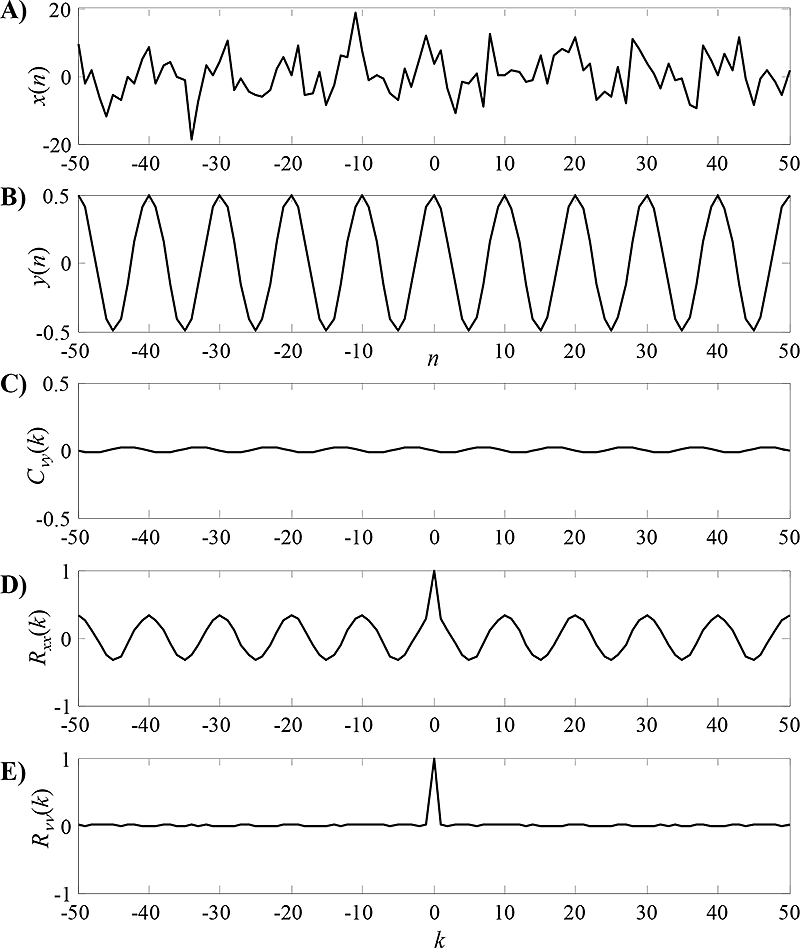
Obr. 6.1: Detekce sinusové vlny skryté v šumu. Amplitudy autokorelačních a křížových korelačních funkcí jsou normované tak, aby nabývaly jedné v počátku. Odhady jsou vypočítané z průběhů dlouhých 10000 vzorků. A) Časová řada x(n) je aditivní směsí užitečné složky s(n) – harmonická časová řada – a rušivé složky v(n) – bílý šum. B) Pomocná časová řada y(n) je harmonická časová řada bez rušení. C) Odhad křížové korelační funkce C_ny(k) ukazuje, že y(n) a v(n) jsou mezi sebou nekorelované. D) Z odhadu autokorelační funkce R_xx(k) časové řady x(n) lze vyčíst jasně periodu užitečné složky ve směsi x(n). E) Odhad autokorelační funkce bílého šumu.

Pomocí pravděpodobnostní funkce lze vyjádřit střední hodnotu časové řady x(n), alternativně k (6.2), jako:

(6.36)

přičemž se někdy uvádí, že pomocí (6.36) je definovaná tzv. očekávaná hodnota (expected value), což je v tomto kontextu jen jiný název pro střední hodnotu náhodné časové řady. Intuitivní důkaz k (6.36) lze ukázat, pokud se v rovnici (6.2) pro časový průměr provede sčítání nikoli přes indexy n, ale přes narůstající amplitudy časové řady x(n). Rozdělením rozsahu všech hodnot x(n) na navazující malé intervaly s šířkou DX centrované v X_i = iDX lze sumu v rovnici (6.2) vyjádřit jako:

(6.37)

Za předpokladu dostatečně úzkých intervalů DX lze všechny hodnoty x(n) v jednotlivých intervalech aproximovat pomocí středu intervalu X_i, a sumu pak lze vyjádřit jako:

Vydělením N a zavedením limity pro velká N se již vyjádří časový průměr:

(6.39)

který za předpokladu velmi úzkých intervalů DX lze vyjádřit pomocí pravděpodobnostní funkce:

(6.40)

neboť pravděpodobnost, že x(n) leží v intervalu o šířce DX centrovaném v X_i lze vyjádřit součinem f_x(X_i)DX. V limitě se suma přes indexy i přibližuje integrálu uvedeném v (6.36).