Boxovy a Jenkinsovy modely stacionárních náhodných procesů

(7.1)

Ukázka empirické autokorelační funkce bílého šumu je na obr. 6.1E. Označení empirická je zde použito proto, že se jedná o odhad teoretické autokorelační funkce náhodného procesu z jedné jeho realizace.

Box-Jenkinsova metodika zahrnuje postup pro konstrukci modelů, který obsahuje tři základní kroky a který odpovídá obecnému postupu uvedenému v úvodním pojednání o náhodných procesech a modelech časových řad. Tři základní kroky jsou pojmenovány jako [1]:

1. Identifikace modelu. Kromě volby struktury modelu zahrnuje tato fáze také zajištění stacionarity časové řady. Detekuje se trendová a periodická složka a případně se aplikuje diferencování časové řady, které je pak zpětně zahrnuto do struktury modelu.
2. Odhad parametrů modelu. Fáze, ve které se vypočítají numerické hodnoty parametrů modelu. Podle typu struktury se využívají lineární nebo nelineární metody nejmenších čtverců a metoda odhadu maximální věrohodnosti.
3. Validace modelu. Fáze, ve které se analýzou residuí (neboli analýzou posloupnosti chyb predikce) ověřuje, zda model dobře vystihuje pozorované dynamické děje popsané časovou řadou.

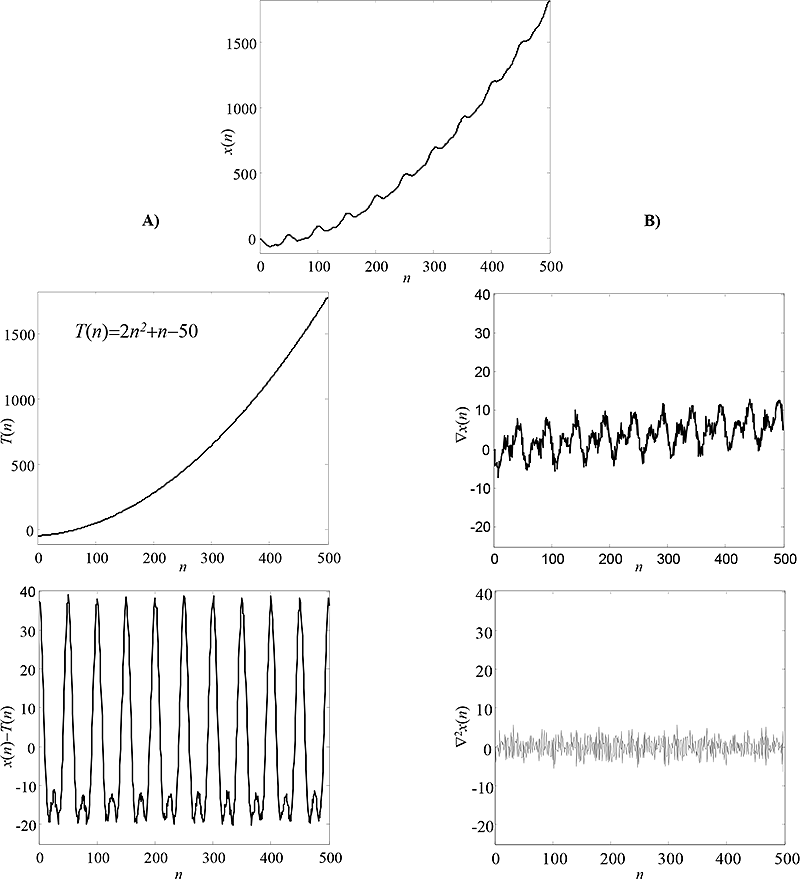
Obr. 7.1: Stacionarizace časové řady x(n): A) odečtením proloženého polynomu, B) jednoduchým a dvojitým diferencováním.

V případě nestacionárních časových řad začíná identifikace modelu předzpracováním časové řady na stacionární posloupnost. Tato fáze je velmi obdobná dekompozici časových řad s následným očištěním časové řady od vlivů zjištěného trendu a případně i očištění od vlivů periodického kolísání. Odstranění trendu může být provedeno odečtením proložené trendové funkce, jak je to naznačeno např. na obr. 7.1A. Jinou možností pro stacionarizaci časové řady je její diferencování, jak je to naznačeno např. na obr. 7.1B. Jednoduché diferencování vede k potlačení lineárního trendu, dvojité diferencování pak očistí časovou řadu od trendu kvadratického. Očištěná posloupnost  vznikne diferencováním posloupnosti x(n) a po konstrukci stacionárního modelu na očištěných datech je pro výpočet  do modelu ještě zahrnuta postupná sumace (integrace) posloupnosti .

Obecný stacionární model ARMA se tak změní na nestacionární model ARIMA (autoregressive integrated moving average). Jednoduché diferencování posloupnosti lze v Z‑transformaci popsat přenosovou funkcí H(z)=1− z⁻¹. Sumaci (integraci) posloupnosti lze v Z-transformaci popsat přenosovou funkcí H(z)=1/(1-z⁻¹), což je přenosová funkce integrační soustavy na mezi stability [3], viz také Systémy a jejich popis v časové a frekvenční oblasti - Lineární časově invariantní systémy a periodické signály, Fourierova řada. Jednoduché diferencování s výše uvedenou přenosovou funkcí lze považovat za lineární filtraci s frekvenční charakteristikou odpovídající filtru typu horní propust, která byla vypočítána v řešené úloze 1, viz obr. 2.4.

Na obr. 2.4 i na obr. 7.1B je vidět, že tato horní propust utlumuje nejen nízkofrekvenční složky odpovídající pozvolným změnám neboli trendu, ale že navíc částečně utlumuje i periodické složky na vyšších frekvencích, které v původní časové řadě x(n) mohou nést užitečnou informaci. Je-li stacionární model ARMA konstruován na takto nevhodně předzpracovaných datech, nebude ani výsledný model ARIMA modelovat dobře všechny dynamické jevy. Tento nedostatek však odborná literatura věnující se Boxovým-Jenkinsovým modelům nezmiňuje a diferencování uvádí jako doporučenou metodu.

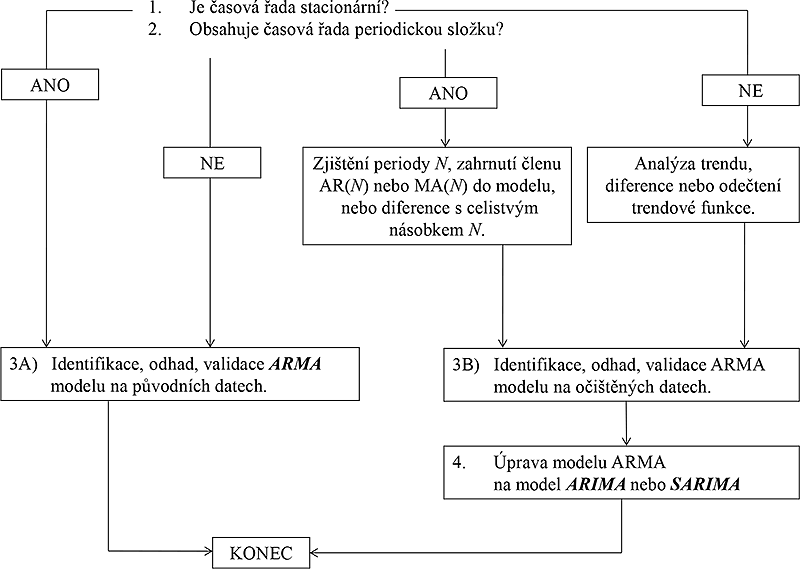
Obr. 7.2: Úprava modelu ARMA na model ARIMA nebo SARIMA v případech konstrukce modelu na  diferencovaných datech. Diferencování časové řady je doporučeno podle Box-Jenkinsovy metodiky v případech, kdy je časová řada nestacionární nebo se v ní vyskytuje
významná periodická složka [1].

Diferencování s celistvým násobkem periody, neboli tzv. sezónní diferencování (seasonal difference, seasonal adjustment) je rovněž součástí fáze identifikace modelu podle Boxovy a Jenkinsovy metodiky, a to v případě, kdy je z nějakého důvodu třeba očistit modelovanou časovou řadu od periodického kolísání jejich hodnot. Je-li sezónní diferencování aplikováno před konstrukcí modelu ARMA, pak je stejně jako v případě jednoduchého nebo dvojitého diferencování pro potlačení trendu nutno tuto operaci zpětně zahrnout do výsledného modelu, který pak bývá označován jako model SARIMA (seasonal ARIMA).

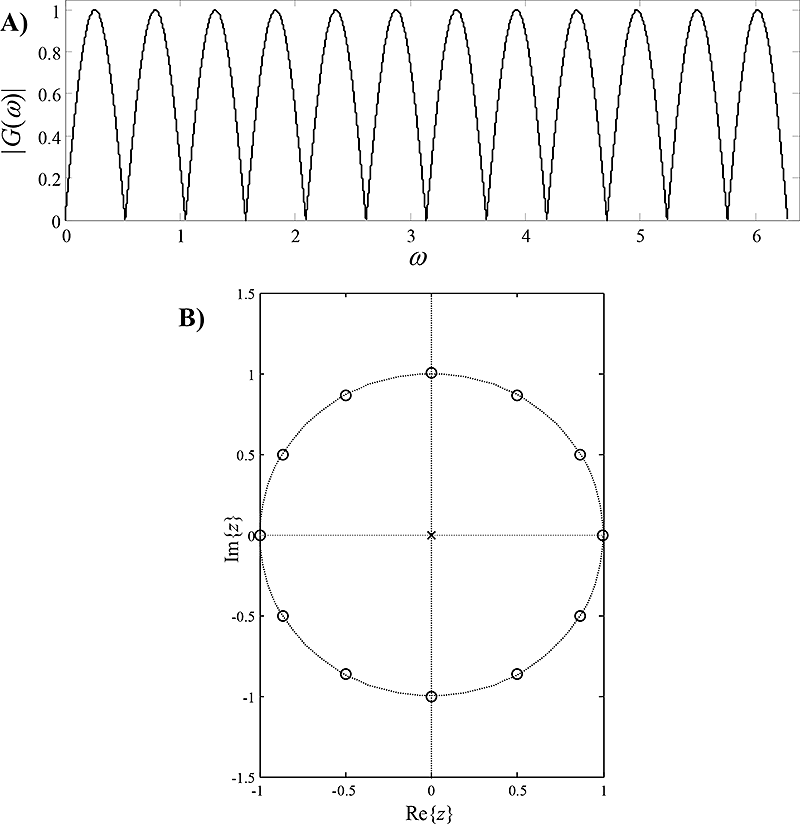
Obr. 7.3: Modulová frekvenční charakteristika (A) a rozložení nulových bodů a pólů (B) diskrétní soustavy realizující tzv. sezónní diferencování pro potlačení periodického kolísání – na uvedeném příkladu se jedná o diferenci s periodou 12 vzorků: . Tato sezónní diference utlumuje děje nejen s periodou 12 vzorků, ale také vyšší harmonické, tj. děje s periodou 6,4,3,2.5 a 2 vzorky.

Tvar přenosové funkce diskrétní soustavy, která realizuje sezónní diferencování, je závislý na délce periody. Např. je-li časová řada x(n) vzorkována s intervalem jeden měsíc, pak jednomu roku odpovídá N=12 vzorků. Je-li cílem analytika dat očistit x(n) od vlivu roční sezóny na sledované jevy a využije-li k tomu sezónní diferencování xd₁₂(n)=x(n)-x(n-12), provádí vlastně lineární filtraci, a to s filtrem s přenosovou funkcí H(z)=1− z⁻¹² , viz frekvenční charakteristiku a rozložení nul a pólů na obr. 7.3. Jedná se o tzv. hřebenový filtr^[2], který si své pojmenování zasloužil podle typicky hřebenového tvaru modulové frekvenční charakteristiky – vlivem rovnoměrného rozložení nulových bodů na jednotkové kružnici. Obr. 7.3 ukazuje, že kromě utlumení základních dějů s periodou 12 měsíců jsou hřebenovým filtrem utlumeny i vyšší harmonické složky a částečný útlum nastává také pro frekvenční složky mezi body nulového a jednotkového přenosu. Analytik by si měl tedy klást před použitím sezónního diferencování otázku, zda zkreslení, které hřebenovým filtrem do očištěné verze časové řady zavede, skutečně nevadí při dalších krocích konstrukce modelu.

Alternativou k sezónnímu diferencování je zahrnutí členu AR(N) nebo MA(N) do modelu, což je jednak ukázáno ve schématu na obr. 7.2 a což také vyplyne z dalšího textu o určování řádů p a q u členů AR(p) a MA(q) v modelu ARMA(p,q).

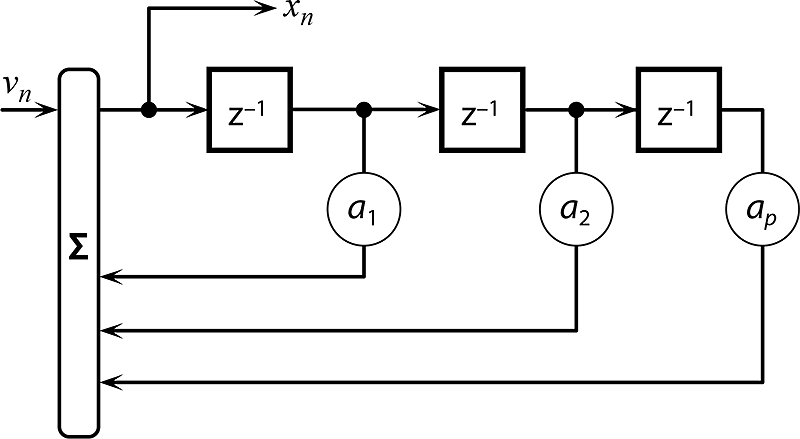
Struktura modelu AR(p) pro stacionární časovou řadu se střední hodnotou  je vyjádřena na obr. 7.4 a v následující rovnici:

(7.2)

Obr. 7.4: Model vzniku časové řady x(n) realizací náhodného procesu AR(p) si lze představit jako IIR filtr řádu p buzený bílým šumem v(n).

Diferenční rovnici (7.2) lze interpretovat jako lineární regresi aktuální hodnoty posloupnosti x(n) proti jedné a více jejím předchozím hodnotám. Jinými slovy lze rovnici popsat tak, že aktuální hodnota časové řady generované náhodným procesem AR(p) je dána lineární kombinací jejich p předchozích hodnot a náhodným přírůstkem v(n), který v čase  s indexem vzorku n tvoří v  procesu jedinou novou informaci.

Struktura modelu MA(q) pro stacionární časovou řadu se střední hodnotu  je vyjádřena na obr. 7.5 a v následující rovnici (7.3). Jde opět o lineární regresi aktuálního vzorku časové řady x(n), ovšem tentokrát ne oproti jejím zpožděným hodnotám, ale oproti hodnotám bílého šumu v(n):

(7.3)

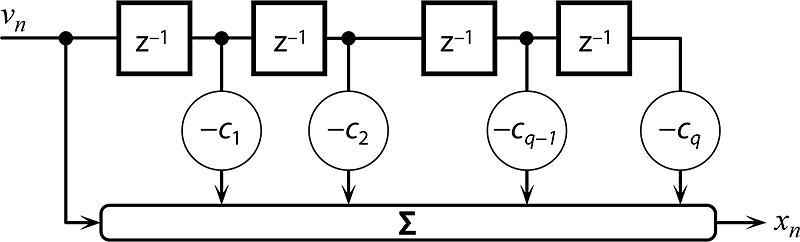
Obr. 7.5: Model vzniku časové řady x(n) realizací náhodného procesu MA(q) si lze představit jako FIR filtr řádu q buzený bílým šumem v(n).

Kombinovaný model ARMA(p, q) pro stacionární časovou řadu se střední hodnotou  v sobě zahrnuje (7.2) i (7.3):

Pro určení struktury a složitosti modelu se využívá zkušeností, experimentování a srovnávání empirické autokorelační funkce pozorované časové řady s teoretickými tvary autokorelačních funkcí vybraných náhodných procesů. Autokorelační funkce stacionárního náhodného procesu je závislá na zpoždění mezi vzorky k a dále na parametrech procesu. Autokorelační funkce autoregresních náhodných procesů mají tvar klesající exponenciály nebo exponenciálně tlumené vlny. U náhodných procesů s klouzavým průměrem autokorelační funkce klesá náhle k nule od určitého konečného zpoždění. Kombinované náhodné procesy ARMA se vyznačují tím, že jejich autokorelace jsou pro úvodní zpoždění k=1,2,…,q komplikovaně závislé na parametrech členů AR i MA, avšak pro zpoždění k>q jsou již závislé pouze na parametrech autoregresního členu, a jejich průběh tedy opět vykazuje tvar klesající exponenciály nebo tlumené vlny. Jednoduchým příkladem je teoretická autokorelační funkce stacionárního náhodného procesu AR(1):

(7.5)

což je vlastně geometrická řada, která monotónně klesá, pokud je parametr a₁ kladný a která má tvar tlumené vlny, pokud je parametr a₁ záporný, viz obr. 7.6.

Tab. 7.1 sumarizuje heuristická pravidla pro určení struktury modelu na základě srovnávání empirických a teoretických autokorelačních funkcí. Pravidla zahrnují také určování řádů p a q, a to na základě parciální autokorelační funkce. Hodnota parciální autokorelační funkce časové řady x(n) pro zpoždění k představuje závislost mezi dvěma vzorky časové řady x(n) a x(n-k), přičemž do této závislosti se nezapočítává lineární vliv vzorků ležících mezi nimi. Jinými slovy se jedná o autokorelační koeficient pro zpoždění k, očištěný od vlivu hodnot vzorků x(n-1), x(n-2),…, x(n-k+1). Podle [2] je parciální autokorelační funkce definována jako:

(7.6)

kde b=[b₁, b₂,… b_k-1] je vektor regresních koeficientů. Průběh parciální autokorelační funkce je využíván pro určování řádu p autoregresního modelu: sleduje se zpoždění, pro které parciální autokorelační funkce nabývá nulové nebo zanedbatelné hodnoty, a hodnota zpoždění předchozího je pak dosazena za p, viz také tab. 7.1.

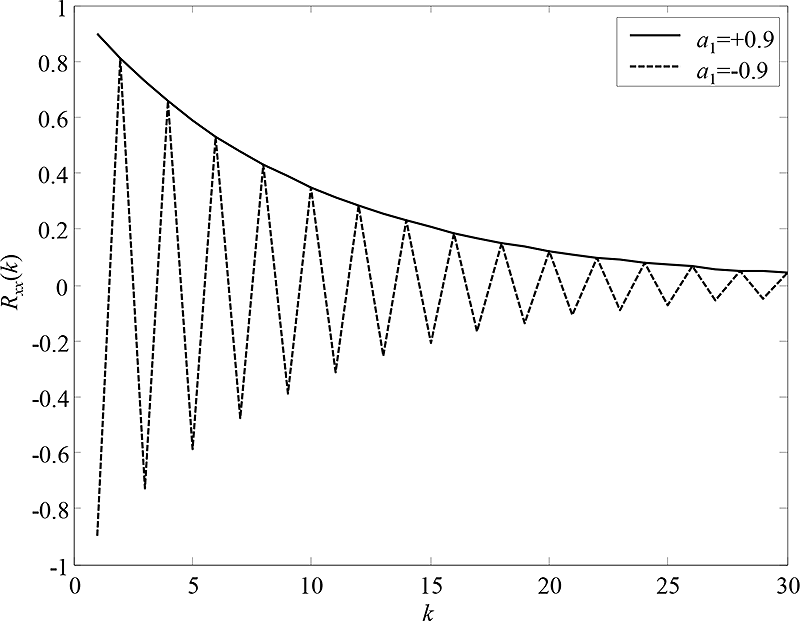
Obr. 7.6: Teoretické průběhy normované autokorelační funkce pro různé parametry
stacionárního náhodného procesu AR(1).

Jednou z metod pro odhad numerických hodnot parametrů ve zvolené struktuře modelu je řešení Yuleho-Walkerových rovnic. V této metodě se rovněž uplatňují autokorelační a autokovarianční funkce náhodných procesů. Autoregresní model řádu p stacionární časové řady s nulovou střední hodnotou lze podle (7.2) zapsat také touto rovnicí:

(7.7)

Pro zavedení autokorelací do rovnice (7.7) se každá strana této rovnice znásobí x(n) a aplikuje se operátor očekávané hodnoty (neboli souborového průměru):

(7.8)

Parametry a_j jsou vytknuty před operátor E, neboť se jedná o deterministické a nikoli náhodné proměnné. Náhodné přírůstky n(n+1) nejsou nijak závislé na předchozích hodnotách x(n), a tak bude druhý člen na pravé straně rovnice (7.8) nulový. Vzhledem k tomu, že autokorelační funkce jsou sudé funkce, lze (7.8) přepsat na:

(7.9)

Pokud se obě strany rovnice (7.7) vynásobí x(n-1), lze stejnými úpravami dospět k rovnici autokorelační funkce pro zpoždění k=2:

(7.10)

Obdobně lze odvodit rovnici autokorelační funkce pro maximální zpoždění mezi vzorky k=p:

(7.11)

Pro všechna možná zpoždění k=1, 2, …, p lze sestrojit následující soustavu Yuleho‑Walkerových rovnic:

	(7.12)
. . .

Soustavu lze přepsat do maticové podoby:

				(7.13)

Stručnější podoba Yuleho-Walkerových rovnic pro autoregresní stacionární náhodné procesy má tvar:

(7.14)

Matice R se označuje také jako autokorelační matice. Jedná se o symetrickou čtvercovou matici s tzv. Toeplitzovou strukturou, která má ve všech klesajících diagonálách shodné prvky. Výpočtem inverzní matice k autokorelační matici R lze vypočítat nebo odhadnout^[3] numerické hodnoty parametrů modelu ve vektoru a:

(7.15)

^[3] Jsou-li autokorelační koeficienty v matici R odhadnuty z pozorovaných časových řad pomocí časových průměrů, nelze hovořit přímo o výpočtu numerických hodnot parametrů modelu, ale raději jen o odhadu parametrů modelu. Pokud jsou k danému náhodnému procesu k dispozici přesné hodnoty autokorelačních koeficientů, nebo je lze vypočítat pomocí souborových průměrů, pak lze hovořit přímo o výpočtu a ne o odhadu parametrů modelu.

^[4] Někteří autoři [1] doporučují ověřovat u residuí jejich normální rozdělení. Definice bílého šumu, viz (7.1), se však neopírá o určité rozdělení pravděpodobnosti. Požadavek na normální rozdělení je tedy dodatečný. Jestliže je rozdělení bílého šumu normální, pak se takový náhodný proces nazývá gaussovský bílý šum [3].