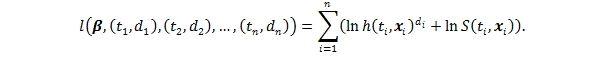Parametrické modely proporcionálních rizik
Pro parametrické modely proporcionálních rizik platí, že má konkrétní vyjádření dané vybraným rozdělením pravděpodobnosti. Předpoklad konkrétního rozdělení je zároveň výhodou i nevýhodou těchto modelů. Znalost rozdělení, z něhož pocházejí pozorované hodnoty, nám umožňuje přesné odhady regresních koeficientů, špatný předpoklad však může vést k nevhodné reprezentaci dat modelem. Pro jednoduchost zde zmíníme pouze dva základní parametrické modely: exponenciální regresní model daný rovnicí
|
|
(7.4) |
a Weibullův regresní model definovaný vztahem
|
|
(7.5) |
Odhad regresních koeficientů parametrického modelu, , je založen na věrohodnostní funkci pro cenzorovaná data, která byla definována v kapitole Parametrické odhady. S použitím výše uvedeného značení se jedná o vztah
|
|
(7.6) |
Ze vztahů (7.4) a (7.5) jsou patrná omezení exponenciálního a Weibullova modelu. Prvním z nich je předpoklad konstantního základního rizika v čase u exponenciálního modelu, který je v případě klinických dat vzácný a každopádně je třeba ho ověřit. V případě Weibullova modelu pak rovnice připouští pouze monotónní základní rizikovou funkci (a z toho plynoucí monotónní rizikové funkce ve všech podskupinách definovaných vysvětlujícími proměnnými), což je někdy z hlediska flexibility popisu dat přežití nedostatečné.