
Weibullovo rozdělení
Weibullovo rozdělení (Weibull distribution) pravděpodobnosti je zobecněním exponenciálního rozdělení, které navrhl Weibull [1] pro popis životnosti materiálů. Na rozdíl od exponenciálního Weibullovo rozdělení nepředpokládá konstantní riziko výskytu sledované události v čase, ale uvažuje monotónní rizikovou funkci (tedy s časem monotónně rostoucí nebo klesající funkci), z čehož plyne také jeho širší uplatnění v praxi. Toto rozdělení je popsáno pomocí dvou parametrů, a
, kde parametr
určuje tvar hustoty pravděpodobnosti Weibullova rozdělení a parametr
škálu hodnot. Spojení Weibullova rozdělení s exponenciálním je následující: Platí-li, že náhodná veličina
umocněná na
se řídí exponenciálním rozdělením s parametrem
, pak
má Weibullovo rozdělení pravděpodobnosti s parametry
a
, tedy lze psát
Pokud se náhodná veličina
řídí podle Weibullova rozdělení s parametry
a
, lze hustotu pravděpodobnosti, rizikovou funkci a funkci přežití popsat vztahy
| (2) | |
Ze vztahu (2) je vidět, že tvar rizikové funkce náhodné veličiny s Weibullovým rozdělením zásadním způsobem závisí na hodnotě parametru , a to takto:
- Pro
je riziková funkce náhodné veličiny
monotónně klesající,
- Pro
je riziková funkce náhodné veličiny
konstantní a tedy
,
- Pro
je riziková funkce náhodné veličiny
monotónně rostoucí.
Jaký tvar křivky má rizikové funkce a funkce přežití při různé volbě parametrů Weibullova rozdělení T je možné vidět na obr: 2.
Rizikovou funkci Weibullova rozdělení tedy není možné specifikovat jako zároveň klesající (např. pro nízké hodnoty veličiny ) a rostoucí (např. pro vysoké hodnoty veličiny
), i tak je toto rozdělení vhodné pro medicínský výzkum, např. pro modelování přežití pacientů s onkologickým onemocněním, u něhož riziko od okamžiku diagnózy s časem monotónně klesá (např. karcinom žaludku, plic), či roste (např. karcinom prsu, prostaty).
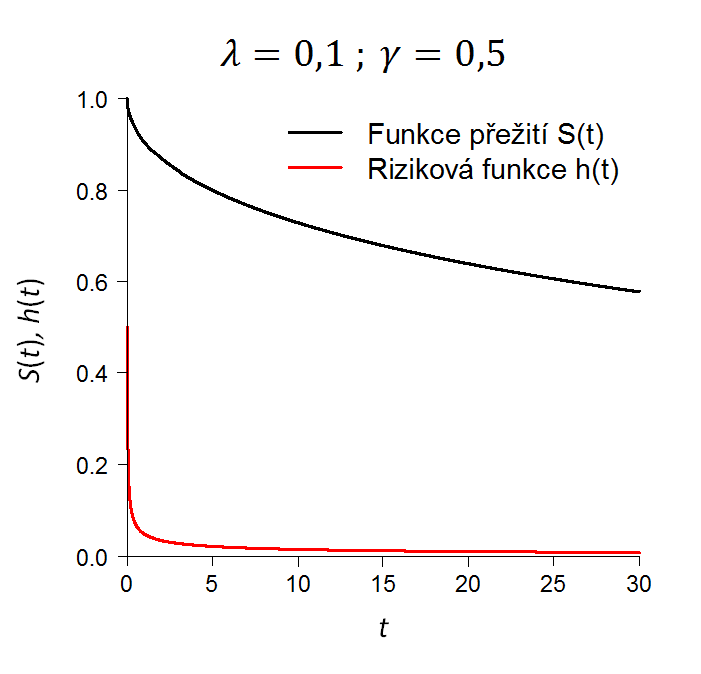
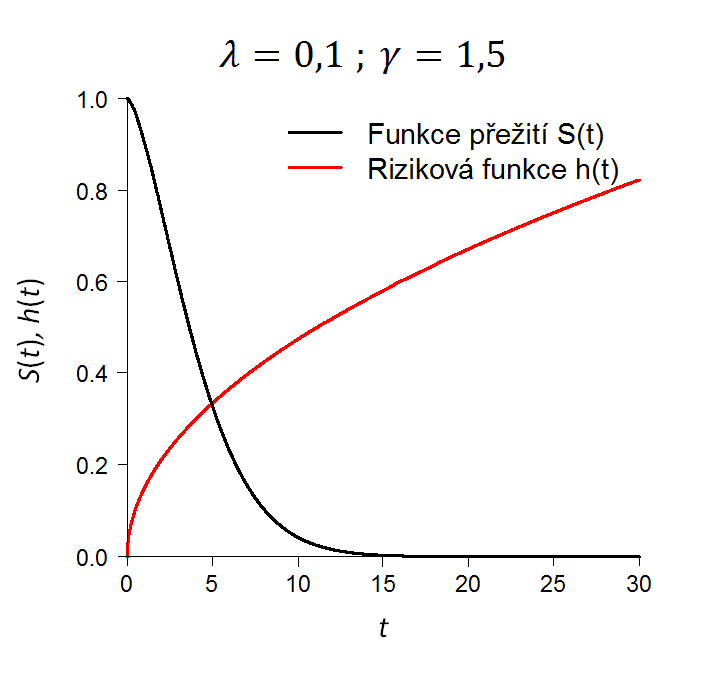
Obr: 2 Funkce přežití a riziková funkce v případě Weibullova rozdělení doby přežití při různé volbě parametrů λ a γ.




