Exponenciální rozdělení

Exponenciální rozdělení (exponential distribution) je spojité rozdělení pravděpodobnosti, které popisuje délky časových intervalů mezi výskyty jednotlivých událostí tzv. Poissonova procesu (Poisson process), což znamená, že popisuje délku časových intervalů mezi jednotlivými událostmi, když se tyto události vyskytují vzájemně nezávisle a s konstantní intenzitou. Tuto intenzitu neboli míru rizika v čase popisuje jediný parametr exponenciálního rozdělení označovaný řeckým . Vysoká hodnota parametru odráží vysoké riziko výskytu sledované události v čase a krátké přežití, zatímco malá hodnota naznačuje opak. Když se náhodná veličina řídí podle exponenciálního rozdělení s parametrem , jsou její hustota pravděpodobnosti, riziková funkce a funkce přežití dány vztahy

	(1)
.

Graf rizikové funkce a funkce přežití v případě exponenciálního rozdělení náhodné veličiny T při různé volbě parametru λ je zobrazen na obr: 1.

Exponenciální rozdělení popisuje čistě náhodný výskyt sledovaných událostí, a proto je někdy označováno jako „rozdělení bez paměti“. To znamená, že čas od začátku sledování neovlivňuje riziko výskytu události v čase, což je vyjádřeno právě konstantní rizikovou funkcí. Ačkoli má exponenciální rozdělení řadu aplikací v technických vědách, jeho použití v řešení klinických experimentů je právě z důvodu konstantní a tudíž neflexibilní rizikové funkce omezené.

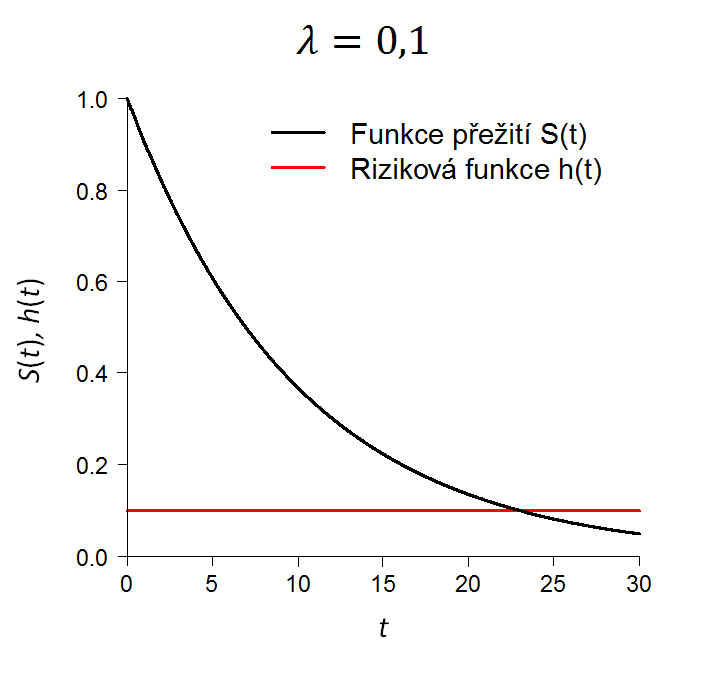
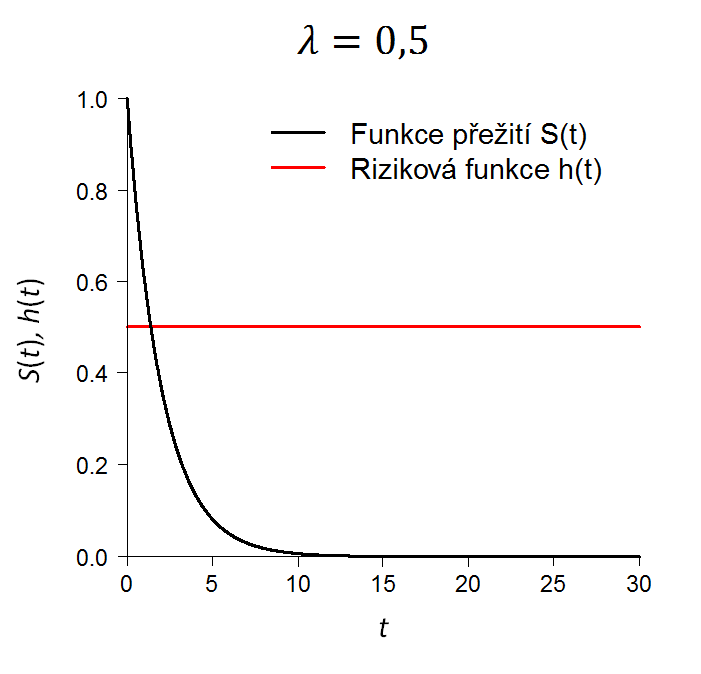
Obr: 1. Funkce přežití a riziková funkce v případě exponenciálního rozdělení doby přežití při různé volbě parametru λ.