Odhad neznámých parametrů uvažovaného rozdělení pravděpodobnosti, které jsou nezbytné pro odhady a , je v analýze přežití založen na metodě maximální věrohodnosti (maximum likelihood estimation). Principem metody maximální věrohodnosti je najít odhad parametru (jmenovitě například parametru exponenciálního rozdělení), který maximalizuje pravděpodobnost, že pozorované hodnoty pocházejí z předpokládaného rozdělení. Jinými slovy se snažíme najít takovou hodnotu , pro niž je pravděpodobnost, že pozorované hodnoty pocházejí z předpokládaného rozdělení, maximální. Odhad se tedy snaží maximálně přizpůsobit pozorovaným časům přežití, což je logické, když připouštíme, že data představují jediný zdroj informací o neznámých parametrech. Sdružená hustota pravděpodobnosti odpovídající realizacím náhodné veličiny , tedy pozorovaným hodnotám , má tvar:

f (t_{1}, \dots, t_{n} | θ) = \overset{n}{\prod_{i = 1}} f (t_{i} | θ)

(5)

Hlavní myšlenkou metody maximální věrohodnosti je dívat se na sdruženou hustotu nikoliv jako na funkci , ale jako na funkci vektoru parametrů (při pevně daných hodnotách ), a vybrat ze všech možných hodnot takové, aby výraz (5) nabýval svého maxima. Pro tento účel zavádíme tzv. funkci věrohodnosti (likelihood function) ve tvaru . Je nutné si uvědomit, že na rozdíl od standardních dat má v přítomnosti cenzorování příspěvek cenzorovaných a kompletních pozorování k funkci věrohodnosti jiný tvar. Když je čas úplným pozorováním, pak příspěvek tého pacienta k věrohodnostní funkci lze vyjádřit jako , což vyjadřuje pravděpodobnost, že se subjekt dožil času bez události a zároveň u něj v čase událost nastala. Když je čas cenzorovaný, pak příspěvek tého pacienta k věrohodnostní funkci lze zjednodušit pouze na , neboť jediné, co víme, je, že se subjekt bez události dožil času . Abychom mohli zohlednit při specifikaci věrohodnostní funkce cenzorování, je třeba pracovat s pozorovanými dvojicemi hodnot . Věrohodnostní funkce v přítomnosti cenzorování pak má tvar

L (θ | (t_{1}, d_{1}), (t_{2}, d_{2}), \dots, (t_{n}, d_{n})) = \overset{n}{\prod_{i = 1}} h {(t_{i})}^{d_{i}} S (t_{i})

(6)

Výpočetně je pro nás však výhodnější maximalizovat logaritmus funkce věrohodnosti (přirozený logaritmus je výhodný pro zjednodušení součinu na součet). Zavádíme tedy tzv. logaritmickou věrohodnostní funkci (log-likelihood function), kterou lze pomocí elementárních úprav vyjádřit ve tvaru

$l (θ \| (t_{1}, d_{1}), (t_{2}, d_{2}), \dots, (t_{n}, d_{n})) = \ln \overset{n}{\prod_{i = 1}} f (t_{i} \| θ) = \ln \overset{n}{\prod_{i = 1}} h {(t_{i})}^{d_{i}} S (t_{i})$
$= \overset{n}{\sum_{i = 1}} (\ln h {(t_{i})}^{d_{i}} + lnS (t_{i}))$	(7)
$= \overset{n}{\sum_{i = 1}} (d_{i} \ln h (t_{i}) - H (t_{i}))$

Příklad 1. S využitím výše uvedeného postupu sestrojíme maximálně věrohodný odhad parametru exponenciálního rozdělení. Věrohodnostní funkce pro exponenciální rozdělení má tvar:

L (λ | (t_{1}, d_{1}), \dots, (t_{n}, d_{n})) = \overset{n}{\prod_{i = 1}} λ^{d_{i}} e^{(- λ t_{i})} .

(8)

Označíme-li celkový počet sledovaných událostí, pak můžeme logaritmus funkce věrohodnosti vyjádřit jako

l (λ | (t_{1}, d_{1}), \dots, (t_{n}, d_{n})) = \overset{n}{\sum_{i = 1}} (d_{i} \ln λ - λ t_{i}) = d \ln λ - λ \overset{n}{\sum_{i = 1}} t_{i} .

(9)

Maximálně věrohodný odhad pak získáme položením derivace tohoto výrazu podle rovno nule, což znamená

{(l (λ | (t_{1}, d_{1}), \dots, (t_{n}, d_{n})))}^{'} = \frac{d}{λ} - \overset{n}{\sum_{i = 1}} t_{i} = 0.

(10)

Výsledným odhadem je pak relativně intuitivní vyjádření odpovídající celkovému počtu pozorovaných událostí, který vztáhneme na celkový pozorovaný osobo-čas v riziku, tedy na celkový součet časů, po něž byly hodnocené subjekty v riziku sledované události:

\hat{λ} = \frac{d}{\sum_{i = 1}^{n} t_{i}}

(11)

Příklad 2. Vhodnost rozdělení pravděpodobnosti popsaných v Metody pro srovnání odhadů přežití na reálná data z klinické praxe demonstrujeme na dvou souborech pacientů s maligním onemocněním. Prvním souborem jsou pacienti s metastatickým karcinomem plic z registru TULUNG, kteří byli léčeni protinádorovou terapií. Odhady funkce přežití sestrojené za předpokladu exponenciálního, Weibullova, logaritmicko-normálního a logaritmicko-logistického rozdělení pravděpodobnosti náhodné veličiny jsou pro tento soubor pacientů znázorněny spolu s neparametrickým Kaplanovým-Meierovým odhadem na obr: 5. Na obrázku je vidět, že logaritmicko-normální a logaritmicko-logistické rozdělení velmi pěkně vystihují neparametrický Kaplanův-Meierův odhad funkce přežití s drobnými výjimkami, které však mohou být způsobeny způsobem sběru dat. Odhady pro exponenciální a Weibullovo rozdělení jsou méně přesné, neboť méně kopírují Kaplanův-Meierův odhad.

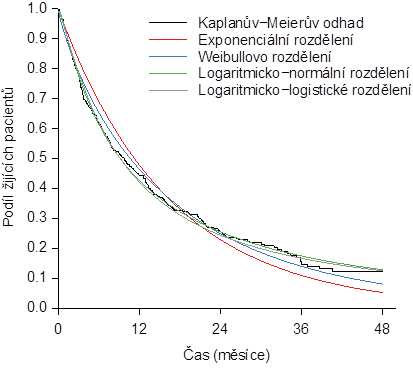Obr: 5. Odhady funkce přežití sestrojené za předpokladu exponenciálního, Weibullova, logaritmicko-normálního a logaritmicko-logistického rozdělení pravděpodobnosti pro soubor pacientů s metastatickým karcinomem plic, kteří byli léčeni protinádorovou terapií.

Druhým souborem jsou pacienti s chronickou myeloidní leukémií z registru CAMELIA, kteří podstoupili transplantaci krvetvorných buněk. Příslušné odhady funkce přežití jsou spolu s neparametrickým Kaplanovým-Meierovým odhadem znázorněny na obr: 6 Z výsledku vidíme, že žádné z uvažovaných rozdělení není na tato data úplně vhodné, neboť se nedokáže vypořádat s poměrně pozvolným klesáním funkce přežití, které je navíc kombinováno s náznakem asymptoty pro funkci přežití po 36. měsíci od transplantace. Funkci přežití, která po určité době od začátku sledování vykazuje asymptotu jinou než 0, je vždy lepší modelovat s pomocí tzv. modelů s podílem statisticky vyléčených pacientů, kterým se věnuje poslední kapitola těchto výukových materiálů.

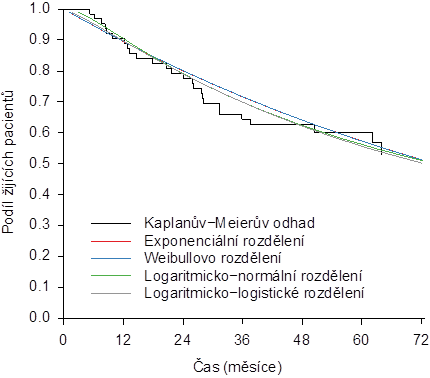Obr: 6. Odhady funkce přežití sestrojené za předpokladu exponenciálního, Weibullova, logaritmicko-normálního a logaritmicko-logistického rozdělení pravděpodobnosti pro soubor pacientů s chronickou myeloidní leukémií, kteří podstoupili transplantaci krvetvorných buněk.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity