Matematické struktury
Matematické struktury, které obsahují proměnné, jež jsou abstrakcí hledaných prvků systému a operátory nad těmito proměnnými a parametry. Operátory mohou reprezentovat algebraické operace, funkce, funkcionály, diferenciální operátory atd. Matematické struktury dělíme podle použitého matematického aparátu z některého odvětví matematiky na analytické, geometrické, topologické, arteficiální a kvalitativní struktury [1]. Pokud jsou operátory v matematickém modelu lineární, hovoříme o lineárních modelech, v opačném případě o nelineárních modelech.
Příklad 1.7: Matematická struktura modelu: homogenní lineární diferenciální rovnice 2. řádu.
Zkoumaný spojitý deterministický model je popsán homogenní lineární diferenciální rovnicí 2. řádu s konstantními koeficienty ve tvaru
Zkoumaný spojitý deterministický model je popsán homogenní lineární diferenciální rovnicí 2. řádu s konstantními koeficienty ve tvaru
V této matematické struktuře máme dvě proměnné: proměnnou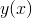 
, která je funkcí druhé nezávisle proměnné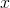 
a obvykle předpokládáme, že nezávisle proměnná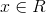
, kde 
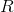je množina reálných čísel. Parametry modelu jsou konstanty 
, 
a 
.
Zkoumaný diskrétní deterministický model je popsán nelineární diferenční rovnicí prvního řádu
a obvykle předpokládáme, že nezávisle proměnná
Zkoumaný diskrétní deterministický model je popsán nelineární diferenční rovnicí prvního řádu
V této matematické struktuře máme proměnnou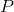 
, která značí např. počet jedinců 
dané
populace a parametry modelu jsou konstanty, .
Hodnoty proměnných mohou být např. reálná, celá nebo binární čísla, booleovské hodnoty nebo textové řetězce. Proměnné mohou být i složitější matematické struktury (např. derivace funkcí, funkce, funkcionály, integrály, posloupnosti, vektory, matice, grafy apod.). Proměnné reprezentují nějaké vlastnosti systému, např. počty jedinců v populaci, výskyt dané události či jevu (ano/ne), výstupy měřených systémů často ve tvaru signálů apod.
populace a parametry modelu jsou konstanty
Hodnoty proměnných mohou být např. reálná, celá nebo binární čísla, booleovské hodnoty nebo textové řetězce. Proměnné mohou být i složitější matematické struktury (např. derivace funkcí, funkce, funkcionály, integrály, posloupnosti, vektory, matice, grafy apod.). Proměnné reprezentují nějaké vlastnosti systému, např. počty jedinců v populaci, výskyt dané události či jevu (ano/ne), výstupy měřených systémů často ve tvaru signálů apod.
