Analýza citlivosti

Analýza citlivosti je velmi důležitá metoda v  procesu implementace, výpočtu a analýze řešení modelu. Bude jí věnována samostatná kapitola. Jejím cílem je na základě změn parametrů modelu vyhodnotit tyto změny v jeho vypočítaném řešení [8]. Tato metoda je obzvláště užitečná k identifikování neurčitostí v modelu, které mohou způsobit jeho nesoulad se zkoumaným systémem. Tento nesoulad pak může být zvýrazněn experimentováním v počítačové simulaci nebo jednoduše popsán a vyznačen při aplikaci modelu.

Pokud je model obzvláště jednoduchý, je možné analyzovat řešení pro každý jeho parametr zvlášť v několika krocích. Tím získáme přesnější odhad změn řešení vázané k jednotlivým parametrům. Ve složitějších modelech je lepší takto nepostupovat a použít některé numerické metody [5].

Příklad 5: Analýza citlivosti parametrů matematického modelu systému výskytu sezónní chřipky v Maple s využitím palety Components a systému MapleCloud

Maple umožňuje analyzovat citlivost parametrů modelu s využitím komponent z palety Componets pomocí interaktivních grafů řešení, viz obr. 9, kde jsou vidět posuvníky (slider) pro parametry
[10-4,9.10-4] a [0.1,0.5] z rovnic (1) - (3) modelu a jejich nastavené hodnoty =0.651807229 10-3 a = 0.2, dále vstupní pole pro nastavení počáteční hodnot Infective(0) = I0 a Suspectible (0) = S0, vytvořené pomocí komponenty MathContainer, kde jsou nastaveny hodnoty I0 = 50 a S0 = 1450. Tento příklad je uložený v systému MapleCLoud, kde je možno na posuvnících měnit parametry a , počáteční hodnoty I0 a S0, a tak interaktivně analyzovat jejich citlivost.
Výpočet se spouští pomocí tlačítka Aktualizuj, které je sdružené s ovládacím programem komponenty Buton v Maple. Způsob jeho vytvoření byl popsán v kapitole o Maple. Program nejprve načte z komponet typu MathContainer pojmenové I0MathContainer a S0MathContainer hodnoty počáteční I0 a S0 a podobně jako v příkladu 3 vykreslí řešení modelu (1) - (4), kde parametry a převezme z komponent typu Slider s využitím balíku DocumentTools:

use DocumentTools in
I0 := Do( %I0MathContainer); #Načte hodnotu I0
S0 := Do( %S0MathContainer); #Načte hodnotu S0
init := Infective(0)=I0, Suspectible(0)=S0, Removed(0)=0;
odesys:= diff(Infective(t),t) = alpha*Infective(t)*Suspectible(t)-beta*Infective(t), diff(Removed(t),t) = beta*Infective(t), diff(Suspectible(t),t) = -alpha*Infective(t)*Suspectible(t);
res:= dsolve([odesys,init],numeric); #výpočet numerického řešení
Do( %Plot=plots[odeplot](res,[[t,Infective(t)], [t,Removed(t)], [t,Suspectible(t)]], 0 .. 40, labels=["t [dny]", "Infective(t),Removed(t),Suspectible(t)"], labeldirections=[horizontal, vertical], title="Počet infekčních lidí se symptomy chřipky (červená křivka)n Počet uzdravených lidí (zelená křivka)n  Počet náchylných lidí (černá křivka)", thickness=2, color=[red, green, black]));
end use;

Pro načtení parametru pomocí komponety Slider pojmenované alphaSLider a výpis jeho hodnoty pomocí komponenty Label pojmenované alphaLabel byl vytvořen ovládací program komponety alphaSlider, který má tvar:

use DocumentTools in
Do(alpha=%alphaSlider(value)); #vstup parameteru α z posuvníku
Do( %alphaLabel(caption)=%alphaSlider(value)); #výpis hodnoty parametru α
init:=Infective(0)=I0, Suspectible(0)=S0, Removed(0)=0;
odesys:= diff(Infective(t), t) = alpha*Infective(t)*Suspectible(t)-beta*Infective(t), diff(Removed(t), t) = beta*Infective(t), diff(Suspectible(t), t) = -alpha*Infective(t)*Suspectible(t);
res:= dsolve([odesys,init],numeric); #výpočet numerického řešení
Do( %Plot=plots[odeplot](res, [[t, Infective(t)], [t, Removed(t)], [t, Suspectible(t)]], 0 .. 40, labels = ["t [dny]", "Infective(t),Removed(t),Suspectible(t)"], labeldirections = [horizontal, vertical], title = "Počet infekčních lidí se symptomy chřipky (červená křivka)n Počet uzdravených lidí (zelená křivka)n  Počet náchylných lidí (černá křivka)", thickness = 2, color = [red, green, black]));
end use;

Pro načtení parametru α pomocí komponety Slider pojmenované betaSLider a výpis jeho hodnoty pomocí komponenty Label pojmenované betaLabel byl vytvořen ovládací program komponety betaSlider, který zde nebude uvádět, neboť je obdobný. Pro oblast grafu se využila komponenta Plot pojmenovaná stejně. Výsledkem je interaktivní zápisník, který je nahrán do systému MapleCloud, kde je možné jej používat k interaktivně analýze citlivosti parametrů , a počátečních hodnot I0 a S0.

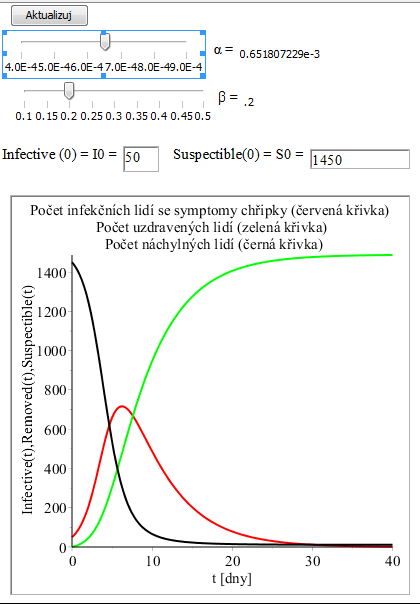
Obr. 10. Interaktivní numerické řešení modelu (1) – (4)

Parametry  a a tím i řešení Infective(t), Removed(t) a Suspectible(t) lze měnit pouze posuvem jezdce na posuvníku (komponetě SLider). U analýzy citlivosti bývá problém jak rozhodnout o velikosti změny každého parametru. Tato změna může záviset na tom, jak přesnou hodnotu parametru chceme získat. Z toho důvodu parametry, které jsou odvozeny ze vstupních dat, mohou obsahovat chyby způsobené jejich odhady. V tom případě je nutné mít procentuální odhad spolehlivosti tohoto odhadnutého parametru. Obzvláště bychom měli dávat pozor na parametry ve vzájemném vztahu, protože změna jednoho z nich může vést k případné změně dalších.