Logické důsledky výrokových formulí
Problém rozhodování, zdali určitá formule vyplývá z množiny formulí
, se nazývá problém dedukce a je jedním ze základních problémů logiky. Ve výrokové logice hovoříme o formuli
, vyplývající z množiny formulí
jako o (tauto)logickém důsledku
. Množina formulí
je nazývána speciální množinou předpokladů, na níž je postavena (z jejích logických důsledků) určitá teorie.
Ohodnocení všech výrokových proměnných vyskytujících se v množině formulí je modelem množiny formulí
, když má pro toto ohodnocení každá formule z
hodnotu true. Pokud má množina formulí
alespoň jeden model, pak je splnitelná, v opačném případě je nesplnitelná.
Příklad:
Najděte modely množiny formulí

Použijeme tabulkovou metodu:
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
* |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
|
* |
1 |
1 |
1 |
1 |
1 |
1 |
Do tabulky zaneseme postupně všechny formule množiny
. Tato množina má dva modely a to na druhém a čtvrtém řádku (označeno hvězdičkami), neboť pro tato ohodnocení mají všechny tři formule z
hodnotu 1(true).
Modely množiny
tedy jsou tato ohodnocení:
1)
2)
Formule je logickým důsledkem množiny
, platí-li pro všechny modely množiny formulí
, že formule
je v nich splněna (má hodnotu true). Někdy také říkáme, že formule
logicky vyplývá z množiny
. Fakt, že formule
je logickým důsledkem množiny
, označujeme
.
Příklad: Ukažte, že formule
je logickým důsledkem formulí
.
Řešení bude provedeno tabulkovou metodou. Zapíšeme-li zadání příkladu symbolicky:
, máme zjistit, zda platí

|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
* |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
* |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
* |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
* |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Jak je vidět z tabulky, formule
je splněna (má hodnotu jedna) pro všechny modely množiny
(viz řádky označené hvězdičkou), proto je jejich logickým důsledkem, neboli formule
vyplývá z předpokladů
.
Poznámka 1: Všimněme si, že formule je splněna (má hodnotu 1) i pro některá ohodnocení, která nejsou modelem množiny
. To nevadí. Nebylo řečeno, že
je log. důsledkem množiny
tehdy, když je splnitelná právě jedině ve všech jejích modelech (což by znamenalo, že v ohodnoceních, která nejsou modely nesmí být splněna), ale, že
musí být splněna ve všech modelech množiny
(což nevylučuje možnost, že by
byla splněna i v ohodnoceních, která nejsou modely).
Poznámka 2: Logický důsledek se vždy vztahuje k nějaké množině předpokladů. Je-li logickým důsledkem množiny
, nemusí být logickým důsledkem množiny
!!! Vše tedy závisí na tom, co říkají předpoklady, na „světě který popisujeme“.
Formule množiny předpokladů nemusí být nutně logicky platné. Je-li však
nesplnitelná množina, pak nemá žádný model a proto jejím logickým důsledkem je libovolná formule. V tom případě lze z
jako důsledek získat formuli
i její negaci
. Nesplnitelná množina předpokladů tedy vede ke sporným důsledkům. Z toho vyplývá, že při zjišťování, zda je formule
logickým důsledkem množiny
musíme nejdříve ověřit, zda je množina formulí
vůbec splnitelná, zda má tedy model.
Modelem prázdné množiny formulí je libovolné ohodnocení výrokových proměnných. Proto logickým důsledkem prázdné množiny formulí může být pouze logicky platná formule (tautologie). Jinými slovy, je-li
prázdná množina formulí, pak
znamená, že
je pravdivá při libovolném ohodnocení, což odpovídá definici tautologie. Tedy symbolický zápis
je zkratkou pro „
je tautologie“. Totéž platí pro logický důsledek množiny
, kterou tvoří pouze tautologie.
Provádíme-li dedukci, pak to znamená, že zjišťujeme, zda z množiny předpokladů vyplývá závěr
. Množina předpokladů
bývá též nazývána množinou hypotéz a
je jejím logickým důsledkem. Tedy:
Připomeňme si, že je-li , hovoříme o platnosti formule
ve všech modelech množiny formulí
.
Následující tvrzení je velmi důležité pro naše další zkoumání. Říká, že problém dedukce lze též formulovat jako logicky platnou formuli
Nechť jsou výrokové formule. Z je logickým důsledkem množiny formulí
, právě když formule
je logicky platná.
Je velmi důležité pochopit, proč je toto tvrzení pravdivé:
Je-li důsledkem množiny
(platí-li
), pak má ve všech modelech množiny U hodnotu 1. Pokud by však formule
neměla být logicky platná, nebo-li by měla mít hodnotu 0, bylo by to tehdy, když hodnota
bude 1 (neboli všechny předpoklady
budou mít hodnotu 1) a hodnota
bude 0 (neboť implikace je nepravdivá, má-li první člen hodnotu 1 a druhý 0). To však nemůže nastat, protože podle definice logického důsledku, mají-li všechny předpoklady
hodnotu 1, pak též závěr
má hodnotu 1 (je v modelu splněn). A my víme, že
je logickým důsledkem, nemůže tedy mít hodnotu 0. Z toho vyplývá, že implikace
je pravdivá.
Také opačně, je-li implikace pravdivá a jsou-li pravdivé všechny předpoklady, musí být pravdivý i závěr
(vyplývá to z pravdivostní tabulky implikace). To ale odpovídá definici logického důsledku Z množiny předpokladů
, proto
.
Co z uvedeného tvrzení vyplývá? Jelikož ověření toho, zda formule je logickým důsledkem množiny
je možno převést na ověření logické platnosti formule
, mnohé nejspíš napadne, že již známe prostředky, jak ověřit, že je tato formule logicky platná. Ano můžeme to udělat (kromě tabulkové metody) také tablovou metodou. Ovšem pro praktické prověřování logických důsledků těmito formálními metodami má větší význam následující tvrzení.
Nechť jsou výrokové formule.
je logickým důsledkem množiny formulí
právě, když množina formulí
je nesplnitelná.
Je zřejmé, že jde-li o splnitelnost množiny formulí, jde v podstatě o současné splnění všech prvků této množiny formulí, tedy o splnění jejich konjunkce. V daném případě jde o konjunkci. Tvrzení tedy jinými slovy říká, že právě tehdy, když konjunkce
není pravdivá.
Jak můžeme této věty využít? Právě jsme zjistili, že je logickým důsledkem množiny formulí
právě, když množina formulí
(neboli konjunkce
) je nesplnitelná. To tedy znamená, že k ověřování logického důsledku můžeme použít jednak tabulkovou metodu a Quinův algoritmus pro formuli
nebo tablovou metodu pro seznam formulí
. Budou li výsledkem tablové metody samé nuly jako hodnoty formule nebo všechny uzly označené hodnotou false u Quinova stromu či jen uzavřené větve u tabla dané formule, pak formule
je logickým důsledkem množiny formulí
.
Právě popsanému typu ověřování logického důsledku se říká nepřímý důkaz, neboť dokazujeme logický důsledek pomocí nesplnitelnost formule . Nepřímý důkaz je často efektivnější a rychlejší než přímý důkaz. Přímý důkaz logického důsledku z množiny formulí by znamenal ukázat, že formule
je logicky platná.
Tedy obecně přímým důkazem se snažíme dokázat logickou platnost, nepřímým nesplnitelnost.
Tablová metoda je dalším ze způsobů, jak ověřit splnitelnost (nesplnitelnost) formule. Tablo reprezentuje postupnou úpravu formule do její disjunktivní normální formy pomocí stromu. V průběhu dochází k postupnému rozkladu formule až na konjunkce jejích literálů. Budeme zde využívat reprezentaci pomocí stromu, grafické znázornění je totiž přehlednější.
Všechny uzly tabla nesou konjunkce formulí, které mají být splněny současně. Místo konjunkcí formulí budeme používat seznamy formulí, to znamená, že místo konjunkce „“ budeme používat čárku „ , “, která bude oddělovat jednotlivé formule. (V celém tablu bude hlavní spojkou konjunkce, proto když pro zjednodušení místo konjunkce budeme používat čárku, nemůžeme si splést její význam. Mějme tedy na paměti, že čárka mezi formulemi vlastně znamená konjunkci těchto formulí). Koncové konjunkce zavěšené na listech jsou buď nesplnitelnými konjunkcemi (tj. takovými, které obsahují komplementární pár literálů) nebo z nich lze stanovit modely formule.
Kořenem stromu představujícího tablo formule je formule v původním tvaru, koncové listy pak obsahují výsledky transformace do disjunktivní normální formy. Každý list představuje jeden disjunkt, který se skládá z konjunkce literálů výrokových proměnných vyskytujících se ve formuli.
Poznámka: Proč je konjunkce zavěšená na listu nesplnitelná, když obsahuje komplementární pár literálů (např. )? Příkladem takového seznamu literálů je např:
což odpovídá vícečlenné konjunkci
. Víme, že vícečlenná konjunkce je pravdivá (true), jestliže jsou všechny její členy pravdivé. Naše konjunkce obsahuje členy
a
, jeden z nich je určitě nepravdivý (jsou dvě možnosti:
, pak
, nebo
, pak
, v obou případech je jeden z nich nepravdivý), proto celá konjunkce je nepravdivá neboli nesplnitelná. Vyplývá to rovněž z ekvivalence (6):
.
Tablová metoda umožňuje úplnou formalizaci postupu ověřování toho, zda je formule splnitelná a je proto jedním z nejperspektivnějších algoritmů pro účely automatického ověřování a odvozování.
Příklad:
Dokažte tabulkovou metodou a tablovou metodou že formule
je logickým důsledkem formulí
. Již jsme to dokázali dříve tabulkovou metodou (přímo). Zde si ji připomeneme, aby byly na jednom příkladě ukázány všechny metody, které již známe a to jak přímo, tak nepřímo.
Symbolicky:
Přímý důkaz: musíme dokázat, že formule
je logicky platná
Nepřímý důkaz: musíme dokázat, že formule
je nesplnitelná
a) přímý důkaz
0
0
0
1
1
0
0
0
1
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
1
0
1
1
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
0
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
Zjistili jsme, že formule
je tautologií, což znamená, že
.
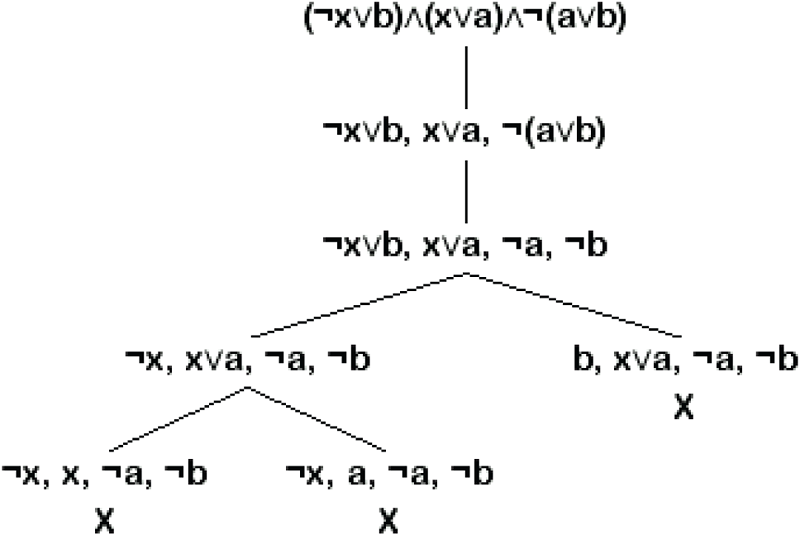
b) nepřímý důkaz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
Zjistili jsme, že formule
je nesplnitelná, což znamená, že
.
Tablová metoda
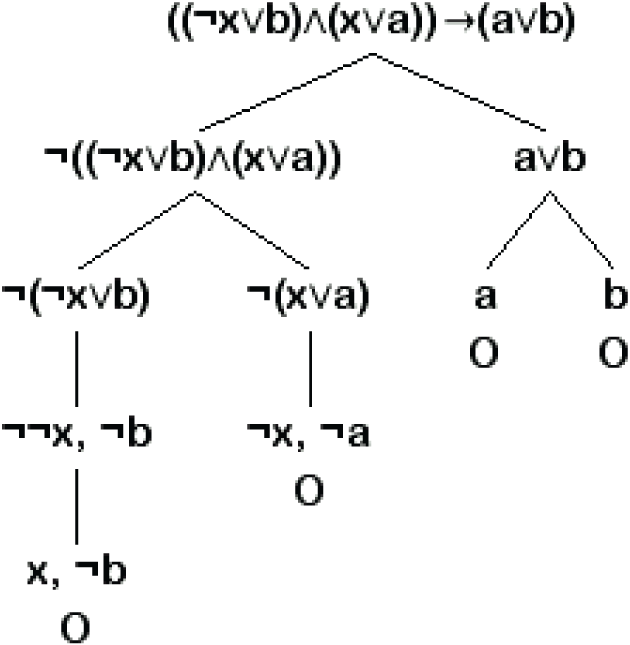
a) přímý důkaz
tablo formule
lze samozřejmě vytvořit, ale pozor: otevřené tablo nedokazuje logickou platnost formule.
b) nepřímý důkaz
vidíme, že tablo formuleje uzavřené, to znamená, že tato formule je nesplnitelná, to však znamená, že
.
Poznámka: u tabulkové metody jsou dvě možnosti, jak dokázat přímou cestou logický důsledek:
-
buď ukázat logickou platnost formule
-
nebo (jak tomu bylo dříve) ukázat, že formule
je splněna ve všech modelech množiny formulí
Z úvah předcházejících odstavců je zřejmé, že za množinu předpokladů lze považovat libovolnou neprázdnou splnitelnou množinu U formulí výrokové logiky. Jak již bylo řečeno, kdyby totiž tato množina formulí byla nesplnitelná, neměla by model a proto by jejím logickým důsledkem byla libovolná formule (zároveň i její negace), což by vedlo ke sporné teorii. Je-li množina předpokladů prázdná, je jejím modelem libovolné ohodnocení výrokových proměnných formule. Proto logickým důsledkem prázdné množiny předpokladů může být pouze logicky platná formule neboli tautologie.
Nyní se podíváme na aplikaci ověřování důsledku na příklad z běžného života.