Floydův algoritmus
Floydův algoritmus slouží především k vyhledání vzdáleností (vzdálenost = délka minimální cesty) v ohodnocených grafech. Algoritmus je založen na porovnání hodnot přímých a nepřímých vzdáleností. Využíváme toho, že hrana 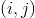 patří do minimální cesty tehdy, pokud nevede minimální cesta jinudy. Zapsáno matematicky:
patří do minimální cesty tehdy, pokud nevede minimální cesta jinudy. Zapsáno matematicky:
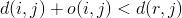
Floydův algoritmus je tvořen z následujícími kroky:
- Sestavení matice přímých vzdáleností
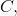 přičemž pro prvky
přičemž pro prvky 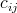 této matice platí:
této matice platí:
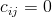 pokud
pokud 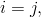
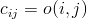 pokud
pokud 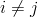 a hrana spojující uzly
a hrana spojující uzly 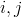 existuje,
existuje,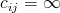 pokud
pokud 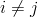 a hrana spojující uzly
a hrana spojující uzly 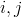 neexistuje.
neexistuje.
- Zavedeme pomocnou proměnnou
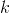 a položíme
a položíme 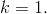 Tato proměnná představuje index vrcholu, pře který provádíme přepočet.
Tato proměnná představuje index vrcholu, pře který provádíme přepočet.
- Provedeme přepočet jednotlivých prvků
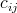 matice
matice 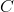 podle pravidla
podle pravidla 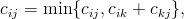 přičemž nepropočítáváme prvky matice, pro které platí
přičemž nepropočítáváme prvky matice, pro které platí 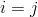 (hlavní diagonála matice), prvky, pro které platí
(hlavní diagonála matice), prvky, pro které platí 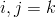 (leží v řádku či sloupci s indexem
(leží v řádku či sloupci s indexem 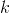 ), a prvky
), a prvky 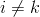 a
a 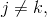 pro které
pro které 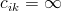 a
a 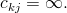
- Pokud
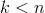 (
(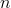 je počet vrcholů grafu), potom položíme
je počet vrcholů grafu), potom položíme 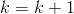 a vracíme se zpět ke kroku 3). Je – li
a vracíme se zpět ke kroku 3). Je – li 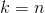 je výpočet ukončen a poslední získaná matice je hledanou maticí vzdáleností.
je výpočet ukončen a poslední získaná matice je hledanou maticí vzdáleností.
Příklad: V zadaném grafu nalezněte vzdálenosti mezi jednotlivými vrcholy pomocí Floydova algoritmu.
Řešení:
|
|
A
|
B
|
C
|
D
|
|
A
|
0
|
|

|

|
|
B
|
3
|
0
|

|
7
|
|
C
|
3
|
2
|
0
|

|
|
D
|

|

|
4
|
0
|
|
|
K=1
|
A
|
B
|
C
|
D
|
|
A
|
0
|

|

|

|
|
B
|
3
|
0
|

|
7
|
|
C
|
3
|
2
|
0
|

|
|
D
|

|

|
4
|
0
|
|
| |
|
K=2
|
A
|
B
|
C
|
D
|
|
A
|
0
|

|

|

|
|
B
|
3
|
0
|

|
7
|
|
C
|
3
|
2
|
0
|
9
|
|
D
|

|

|
4
|
0
|
|
| |
|
K=3
|
A
|
B
|
C
|
D
|
|
A
|
0
|

|

|

|
|
B
|
3
|
0
|

|
7
|
|
C
|
3
|
2
|
0
|
9
|
|
D
|
7
|
6
|
4
|
0
|
|

patří do minimální cesty tehdy, pokud nevede minimální cesta jinudy. Zapsáno matematicky:
přičemž pro prvky
této matice platí:
pokud
pokud
a hrana spojující uzly
existuje,
pokud
a hrana spojující uzly
neexistuje.
a položíme
Tato proměnná představuje index vrcholu, pře který provádíme přepočet.
matice
podle pravidla
přičemž nepropočítáváme prvky matice, pro které platí
(hlavní diagonála matice), prvky, pro které platí
(leží v řádku či sloupci s indexem
), a prvky
a
pro které
a
(
je počet vrcholů grafu), potom položíme
a vracíme se zpět ke kroku 3). Je – li
je výpočet ukončen a poslední získaná matice je hledanou maticí vzdáleností.





