
Sémantika jazyka predikátové logiky (interpretace formulí)
Sémantika neboli význam formulí predikátové logiky 1. řádu, je dána jejich interpretací. Položíme-li si otázku zda daná formule predikátové logiky je pravdivá či ne, pak taková otázka je v podstatě nesmyslná, pokud nevíme, co formule znamená, tedy jak je interpretována. Tak např. formule
může ”říkat”, že pro všechna přirozená čísla platí, že jejich druhá mocnina je větší než to číslo, nebo že pro všechny lidi platí, že jejich otec je starší než dotyčný člověk, pak je samozřejmě v takových interpretacích pravdivá. Může ale také znamenat, že pro všechna přirozená čísla platí, že jejich druhá mocnina je menší než to číslo, nebo že pro všechny lidi platí, že jejich otec je mladší než dotyčný člověk, pak je samozřejmě (v takové interpretaci) nepravdivá.
Podobně např. formule, kterými jsme v předchozí kapitole analyzovali věty přirozeného jazyka, mohou být interpretovány tak, aby zachycovaly význam těchto vět (”zamýšlená” interpretace), ale mohou být interpretovány úplně jinak. Například formule, která je analýzou věty Někteří chytří lidé jsou líní, tedy
může být interpretována jako zachycující význam věty Některá lichá čísla jsou dělitelná dvěma, a pak je evidentně (v této interpretaci) nepravdivá.
V čem tedy spočívá interpretace formule? Nejprve musíme stanovit, ”o čem mluvíme”, tedy jaká je předmětná oblast - obor proměnnosti proměnných, tj. zvolíme jistou neprázdnou množinu – univerzum, jejíž prvky budou individua. Jelikož predikátové symboly mají vyjadřovat vztahy mezi těmito předměty - prvky univerza, přiřadíme každému -árnímu predikátovému symbolu jistou
-ární relaci (tj. podmnožinu Kartézského součinu) nad univerzem. Jedná-li se o unární predikátový symbol
, pak přiřadíme podmnožinu univerza. Podobně funkční symboly budou vyjadřovat
-ární funkce nad univerzem. Teprve poté, co je daná formule interpretována, můžeme vyhodnotit její pravdivost či nepravdivost v dané interpretaci. Je zde však ještě jeden problém, a to jsou proměnné. Proměnným jazyka predikátové logiky přiřazujeme valuací individua, tj. prvky univerza. (Proměnným jazyka predikátové logiky druhého řádu pak mohou být přiřazeny také vlastnosti či funkce.) Pravdivostní hodnota formule nezávisí na hodnotě vázaných proměnných (pouze volné proměnné jsou ”skutečné” proměnné). Obsahuje-li však formule nějaké volné proměnné, můžeme vyhodnotit její pravdivost v interpretaci pouze v závislosti na ohodnocení (valuaci) volných proměnných. Při některé valuaci může být formule v dané interpretaci pravdivá, při jiné nepravdivá. Tak např. formule
může být interpretována nad množinou celých čísel tak, že symbolu je přiřazena relace větší nebo rovno
, symbolu
funkce druhá mocnina (tedy
”znamená”
). Pak formule ”říká”, že pro každé celé číslo
platí, že
je větší než nebo rovno jistému číslu
. Tedy pravdivost formule v této interpretaci závisí na ohodnocení (valuaci) proměnné
. Přiřadíme-li např.
číslo 5, je formule nepravdivá, přiřadíme-li třeba číslo -3 nebo 0, je formule pravdivá. Obecně bude formule pravdivá (v této interpretaci) pro každou valuaci proměnné
, která přiřadí
záporné číslo nebo nulu, nepravdivá pro všechny valuace, které přiřadí proměnné
číslo kladné.
Níže jsou pravidla, která použijeme při interpretaci jazyka predikátové logiky (tzv. interpretační pravidla):
-
Individuálním proměnným je přiřazena neprázdná množina
(univerzum) jako jejich definiční obor hodnot. Všechny individuální proměnné mají tedy tutéž interpretaci.
-
Každému
-árnímu funkčnímu
symbolu jazyka přiřadíme určité zobrazení
. Každý
-ární funkční symbol je tedy interpretován jako funkce, která přiřazuje
-tici individuí právě jedno individuum, tj. zobrazení z
do
. Specielně pak platí že:
- je-li
, pak se jedná o nulární funkční symbol, tedy o individuovou konstantu, které je přiřazen prvek univerza - individuum
- je-li
, pak se jedná o unární funkční symbol, kterému je přiřazena funkce o jednom argumentu (např. nad množinou čísel
,
, nad množinou individuí otec
, matka
, atd.)
- je-li
, pak se jedná o binární funkční symbol, kterému je přiřazena binární funkce se dvěma argumenty (např. nad množinou čísel
,
, atd.)
-
Každému
-árnímu predikátovému symbolu
přiřadíme jistou
-ární relaci
nad
, tj podmnožinu Kartézského součinu
(tj.
), neboli zobrazení
. Tato relace
se nazývá obor pravdivosti predikátu. Specielně pak platí že:
- je-li
, pak se jedná o nulární predikátový symbol, kterému je přiřazena hodnota 1 nebo 0 (pravda, nepravda) tak, jak to již známe z výrokové logiky.
- je-li
, pak se jedná o unární predikátový symbol, kterému je přiřazena podmnožina univerza
. (Vlastnosti tedy v predikátové logice vyjadřujeme jako podmnožiny univerza.)
- je-li
, pak se jedná o binární predikátový symbol, kterému je přiřazena binární relace nad univerzem (např. relace větší, menší, apod.)
Výroková logika je tedy specielním (nejjednodušším) případem predikátové logiky, a to 0. řádu, ve které pracujeme pouze s nulárními predikáty a nepotřebujeme proto termy, funkční symboly, individuové proměnné ani univerzum. Nulárním predikátům přiřazujeme pouze hodnoty pravda, nepravda.
Příklad: Uvažujme jazyk predikátové logiky s následujícími konstantami:
,
- nulární funkční symboly
- unární funkční symbol
- binární funkční symboly
binární predikátové symboly.
Pro tento jazyk definujme interpretaci následujícím způsobem:
- Univerzum M je množina všech nezáporných celých čísel
.
Realizace funkčních symbolů jsou definovány takto:
... předmětová konstanta: číslo 0 /nikoliv pravdiv. hodnota !/
... předmětová konstanta: číslo 1 /nikoliv pravdiv. hodnota !/
... zobrazení
definované takto:
... zobrazení
definované takto:
... zobrazení
definované takto:
Realizace predikátových symbolů jsou definovány takto:
... podmnožina množiny
definovaná jako množina všech dvojic
, pro které platí
,
... podmnožina množiny
definovaná jako množina všech dvojic
, pro které platí
.
Skutečnost, že např. pro všechna
zapíšeme standardní formulí predikátové logiky takto:
Můžeme přirozeně použít i obvyklého nestandardního zápisu, který využívá speciální infixovovou notaci binárních funkcí a další speciální konvence (např. priorita násobení před sčítáním).
Informaci, že ke každým dvěma číslům x, y existuje číslo z takové, že buď nebo
zapíšeme formulí:
Nebo také standardně:
Definice: Ohodnocení (valuace) individuových proměnných je zobrazení , které každé proměnné
přiřazuje hodnotu
(prvek univerza)
Definice: Ohodnocení termů indukované ohodnocením proměnných
je induktivně definováno takto:
, kde
je funkce přiřazená v dané interpretaci funkčnímu symbolu
.
Poznámka: Hodnotou (realizací) termu t v interpretaci I je tedy vždy jistý prvek univerza. Tedy funkční symboly jsou “jména funkcí – zobrazení”, termy jsou “jména prvků univerza”, zatímco predikátové symboly jsou “jména relací” a formule jsou “jména pravdivostních hodnot”.
Definice: Pravdivost formule v interpretaci
pro ohodnocení e individuových proměnných (což značíme
– formule
je pravdivá v
pro
, nebo také
je splněna v
ohodnocením
), je definována v závislosti na tvaru formule:
-
Je-li
atomická formule tvaru:
-
, kde p je predikátový symbol (různý od =) a
jsou termy, pak
, jestliže platí
, kde
je relace přiřazená interpretací
symbolu
– obor pravdivosti
. Tedy individua, která jsou hodnotou termů
, jsou v relaci
.
-
, pak
, jestliže platí
, tj. oba termy jsou realizovány týmž individuem.
-
-
Je-li
složená formule, pak na základě jejího tvaru platí:
-
, pak
jestliže neplatí
-
, pak
, jestliže platí
a
-
, pak
, jestliže platí
nebo
-
, pak
, jestliže neplatí
nebo platí
-
, pak
, jestliže platí
a
, nebo neplatí
a neplatí
-
-
je-li
formule tvaru:
-
, pak
, jestliže pro libovolné individuum i
platí
, kde
je valuace stejná jako e až na to, že přiřazuje proměnné
individuum
.
-
, pak
, jestliže pro alespoň jedno individuum i
platí
, kde
je valuace stejná jako e až na to, že přiřazuje proměnné
individuum
.
-
Poznámka: Je-li univerzum konečná množina , pak platí následující ekvivalence formulí:
Definice: Formule je splnitelná v interpretaci
, jestliže existuje ohodnocení e proměnných takové, že platí
.
Definice: Formule je pravdivá v interpretaci
, značíme
, jestliže pro všechna možná ohodnocení
individuových proměnných platí, že
.
Definice: Formule je splnitelná, jestliže existuje interpretace
, ve které je splněna, tj. jestliže existuje interpretace
a valuace
takové, že
. Taková interpretace
a valuace
, tedy dvojice
, pro kterou platí
, se nazývá model formule.
Definice: Formule je tautologií (logicky pravdivá), značíme
, jestliže je pravdivá v každé interpretaci.
Definice: Formule je kontradikcí, jestliže nemá model, tedy neexistuje interpretace
, která by formuli
splňovala.
Poznámka: Zjevně platí, že je kontradikce, právě když negace
je tautologie,
.
Definice: Model množiny formulí je taková interpretace
(a případně valuace
volných proměnných), která splňuje všechny formule
, tedy dvojice
, pro kterou platí
.
Definice: Formule logicky vyplývá z formulí
, značíme
, jestliže
je pravdivá v každém modelu množiny formulí
.
Tedy pro každou interpretaci , která splňuje formule
platí, že splňuje také formuli
.
Příklad:
Uvažujme jazyk predikátové logiky a jeho interpretaci z minulého příkladu.
Formule , neboli
je pravdivá v uvedené interpretaci např. pro ohodnocení proměnných
,
a nepravdivá např. pro ohodnocení
,
. Formule je splnitelná v dané interpretaci, není však v této interpretaci pravdivá.
Formule, neboli
je v uvedené interpretaci pravdivá pro každé ohodnocení a je tedy, stejně tak jako formule
, neboli
pravdivá v této interpretaci. Není však univerzální logickou tautologií (interpretujeme-li např. binární predikát p jako ostrou nerovnost, pak uvedené formule jsou nepravdivé).
Formule , neboli
je pravdivá v dané interpretaci a formule
, neboli
je nesplnitelná v dané interpretaci jazyka predikátové logiky.
Formule jsou pravdivé v dané interpretaci, nejsou však univerzálními logickými tautologiemi (o tom se přesvědčíme např. tak, že prohodíme interpretaci predikátů
a
).
Formule jsou univerzálními tautologiemi daného jazyka. Jejich pravdivost nezávisí na tom, jakou množinu probíhají předmětové proměnné, jak je interpretován funkční symbol
a jak je interpretován predikátový symbol
. Naproti tomu formule
nejsou splnitelné v žádné interpretaci a jsou tedy univerzálními kontradikcemi.
Úloha: Ukažte, že formule , kde
je individuová konstanta, není tautologií, ale je splnitelná.
Jelikož formule nemá volné proměnné, stačí nalézt interpretaci, ve které je pravdivá, a interpretaci, ve které není pravdivá.
Formule je pravdivá například v následující interpretaci:
- univerzum
= množina přirozených čísel
= množina lichých čísel
= 3
Formule je pravdivá například v následující interpretaci:
- univerzum
= množina přirozených čísel
= množina lichých čísel
= 4
Formule je tedy je splnitelná, ale nejedná se o tautologii.
Definice: Formule jsou (sémanticky) ekvivalentní, jestliže pro všechny interpretace
a všechny valuace e mají stejná pravdivostní ohodnocení. Skutečnost, že formule
jsou ekvivalentní zapisujeme:
.
Níže jsou uvedeny některé důležité tautologie predikátové logiky:
- Všechny formule predikátové logiky mající tvar tautologií výrokové logiky, např. formule
je tautologií, protože má tvar formule výrokové logiky
, která je tautologií výrokové logiky.
-
De Morganovy zákony:
-
Zákony distribuce kvantifikátorů:
-
Zákony prenexních operací (předpokládáme, že formule A neobsahuje volnou proměnnou
):
-
Zákony komutace kvantifikátorů:
-
Nechť term
je substituovatelný za proměnnou
, pak platí
zákon konkretizace
zákon abstrakce
zákon partikularizace
Sémantické ověření správnosti úsudku je v predikátové logice obtížnější než ve výrokové logice. Podle definice je úsudek správný, pokud je závěr pravdivý ve všech modelech předpokladů. Problémem v predikátové logice je ovšem ten, že takovýchto modelů je obecně nekonečně mnoho. Přesto je možno sémanticky ověřit platnost úsudku, a to přímo, nebo pak nejčastěji sporem (předpokládáme, že může nastat případ, kdy v nějaké interpretaci budou předpoklady pravdivé a závěr nepravdivý a ukážeme, že to možné není).
Příklad: Sémanticky ověřte správnost úsudku:
Marie má ráda pouze vítěze.
Karel je vítěz.
––––––––––––––––––––––
Marie má ráda Karla.
Řešení:
Úsudek zformalizujeme:
––––––––––––––––
Aby byly předpoklady pravdivé, pak možné interpretace nad množinou individuí musí mít tvar:
: Marie,
: Karel (poznámka: realizací těchto konstant mohou být kterékoli jiné prvky D, avšak celková úvaha se tím nijak nemění.)
Vidíme, že závěr nevyplývá, neboť není zaručeno, že relace bude obsahovat dvojici
.
Poznámka: Tento úsudek ilustruje poměrně častou chybu, které se můžeme v argumentaci dopustit. Z platnosti nutné podmínky nějakého tvrzení usuzujeme na pravdivost tohoto tvrzení. V našem příkladě je podmínka ”být vítězem” pouze nutná, ne však dostatečná pro to, aby Marie měla dané individuum ráda (vítězové tedy mohou být i taková individua, která Marie nemá ráda).
Příklad: Sémanticky ověřte správnost úsudku:
Marie má ráda pouze vítěze.
Karel není vítěz.
––––––––––––––––––––––
Marie nemá ráda Karla.
Řešení:
Úsudek zformalizujeme:
––––––––––––––––
Aby byly předpoklady pravdivé, pak možné interpretace nad množinou individuí musí mít tvar:
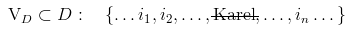 - individuum Karel neleží v množině
- individuum Karel neleží v množině , tedy Karel se nerovná žádnému z individuí
které jsou v relaci
s individuem Marie.
Vidíme, že závěr vyplývá, neboť je zaručeno, že relace nemůže obsahovat dvojici
.




