Autonomní rovnice závislé na parametru

Nechť nyní kde je funkce dvou proměnných taková, že pro každé a každé platí Pro pevně zvolené můžeme funkci chápat jako funkci jedné proměnné a považovat za parametr. Tuto funkci jedné proměnné budeme značit

Uvažujme rekurentní formuli

(13)

Řekneme, že při hodnotě parametru dochází k bifurkaci, pokud existuje takové, že pro je řešení rovnice  Autonomní rovnice (13) „kvalitativně odlišné“ od řešení této rovnice pro

Poněkud vágně zavedený pojem „bifurkace“ nejprve ilustrujme dvěma příklady.

Příklad 2.17.
Uvažujme logistickou rovnici

(14)

s parametrem Tato rovnice má rovnovážné body a Vyšetříme jejich stabilitu. Platí

Podle věty Autonomní rovnice 2.12 vidíme, že pro resp. pro je rovnovážný bod stabilní, resp. nestabilní. Dále platí pro pro a pro takže rovnovážný bod je pro stabilní a pro nestabilní.

Při hodnotě tedy dochází k bifurkaci: pro hodnoty parametru  v levém okolí je rovnovážný bod asymptoticky stabilní a rovnovážný bod je nastabilní; pro hodnoty v pravém okolí je naopak stacionární bod nestabilní a stacionární bod asymptoticky stabilní. Bifurkaci při hodnotě lze popsat tak, že rovnovážné body si vymění stabilitu. Taková bifurkace se nazývá transkritická.

K bifurkaci dochází také při hodnotě parametru pro hodnoty parametru v levém, resp. pravém, okolí hodnoty je stacionární bod asymptoticky stabilní, resp. nestabilní. Bifurkaci při hodnotě parametru lze popsat jako ztrátu stability rovnovážného bodu.

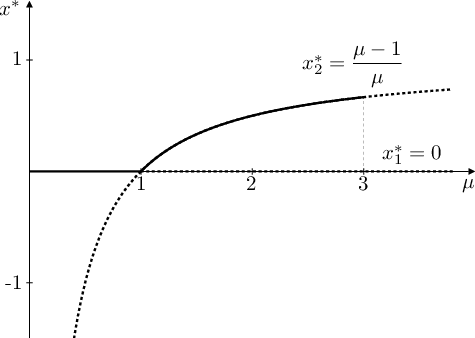
Situaci lze graficky znázornit jako závislost stacionárních bodů rovnice na parametru , viz obr. Autonomní rovnice 6 vlevo. Je-li rovnovážný bod asymptoticky stabilní, znázorníme průběh jeho hodnot plnou čarou, je-li nestabilní, znázorníme ho tečkovaně.

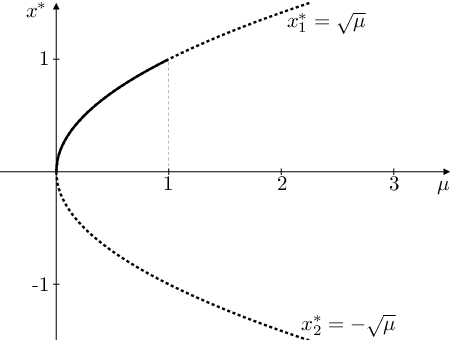
Obr. 6. Rovnovážné body logistické rovnice Autonomní rovnice (14) (vlevo) a rovnice Autonomní rovnice (15) (vpravo) v závislosti na hodnotách parametru Asymptoticky stabilní rovnovážný bod je znázorněn plnou čarou, nestabilní tečkovanou čarou.

Příklad 2. 18. Uvažujme rovnici

(15)

Její rovnovážné body jsou řešením kvadratické rovnice

Pro parametr tedy rovnice  Autonomní rovnice (15) rovnovážné body nemá a pro má dva rovnovážné body Při hodnotě parametru tedy dochází k bifurkaci.

Podívejme se na stabilitu rovnovážných bodů v případě Platí

Rovnovážný bod je nestabilní a rovnovážný bod je pro asymptoticky stabilní a pro je nestabilní. Při hodnotě parametru tedy také dochází k bifurkaci.

Bifurkace rovnice Autonomní rovnice (15) lze popsat tak, že při růstu parametru se při překročení hodnoty objeví dva rovnovážné body, z nichž jeden je asymptoticky stabilní a druhý nestabilní; dále při překročení hodnoty stabilní rovnovážný bod stabilitu ztratí. Situaci lze opět znázornit graficky, viz obr. Autonomní rovnice 6 vpravo.

Bifurkační diagram představuje jinou možnost, jak znázornit kvalitativní vlastnosti řešení rovnice Autonomní rovnice (13) v závislosti na parametru. V něm jsou na vodorovné ose zobrazeny hodnoty parametru a na svislé ose je zobrazen atraktor rovnice pro příslušnou hodnotu parametru.

Konstrukci bifurkačního diagramu můžeme popsat následujícím algoritmem:

1. Specifikujeme hodnoty parametru Zvolíme čas který budeme považovat za dobu, během níž se „chování řešení ustálí“, a maximální čas
2. Položíme
3. Položíme a zvolíme
4. Najdeme řešení rovnice Autonomní rovnice (13) s počáteční podmínkou pro indexy tj. najdeme množinu
5. Zakreslíme množinu bodů
6. Pokud zvětšíme o jedna a vrátíme se k bodu 3.

Obr. 7. Bifurkační diagram logistické rovnice Autonomní rovnice (14).

Na obrázku Autonomní rovnice 7 je populární bifurkační diagram logistické rovnice Autonomní rovnice (14). Hodnoty parametru jsou voleny v rozpětí až s ekvidistantním krokem délky čas „pro ustálení řešení“ je maximální čas Na diagramu je dobře vidět stabilní rovnovážný bod pro stabilní 2-cyklus pro stabilní 4-cyklus pro a stabilní 3-cyklus pro Pro hodnotu parametru atraktor logistické rovnice Autonomní rovnice (14) hustě vyplňuje celý interval