Analýza rovnice Aplikace (75) v autonomním případě

Předpokládejme, že poměr počtu zygot určitého genotypu v časovém intervalu a počtu gamet vyprodukovaných jedincem téhož genotypu v čase je stejný pro každý čas V takovém případě jsou podle Aplikace (73) reprodukční zdatnosti jednotlivých genotypů a konstantní, jsou to nezáporné parametry rovnice Aplikace (75). Budeme předpokládat, že alespoň jeden z parametrů je kladný. V opačném případě by totiž uvažovaná populace vymizela hned v první filiální generaci.

Nejprve uvažujme kladné reprodukční zdatnosti heterozygotů, Zavedeme relativní zdatnosti homozygotů vzhledem ke zdatnosti heterozygotů

Zlomek na pravé straně rovnice Aplikace (75) vykrátíme parametrem a upravíme. Dostaneme rovnici

(81)

se dvěma nezápornými parametry. Poněvadž stavová proměnná vyjadřuje relativní frekvenci (tj. pravděpodobnost), je stavovým prostorem uzavřený interval

Při analýze rovnice Aplikace (81) rozlišíme tři případy.

(i) reprodukční zdatnosti všech genotypů jsou stejné. V tomto případě je rovnice Aplikace (81) tvaru

která má jedině konstantní řešení. Pokud tedy reprodukce nezávisí na genotypu, frekvence alel v populaci se nemění. To je Hardyho-Weinbergův zákon.

(ii.) a  reprodukční zdatnost homozygota genotypu je stejná, jako reprodukční zdatnost heterozygota a reprodukční zdatnost homozygota genotypu je jiná. Jinak řečeno, jedinci genotypů a mají stejný fenotyp, jedinci genotypu mají fenotyp jiný. To odpovídá situaci, že alela je dominantní a alela  je recesivní. V tomto případě má rovnice Aplikace (81) tvar

(82)

Najdeme její rovnovážné body a vyšetříme jejich stabilitu.

Označme na chvíli Rovnice má dva kořeny a Platí

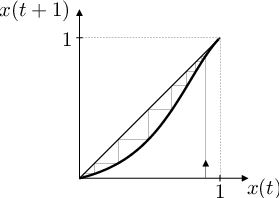
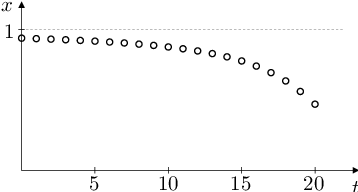
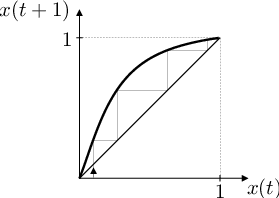
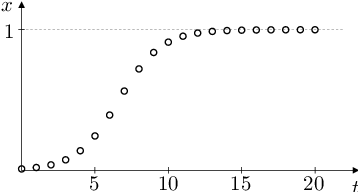
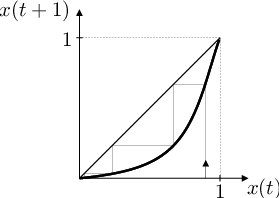
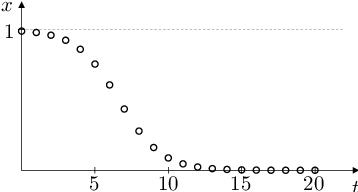
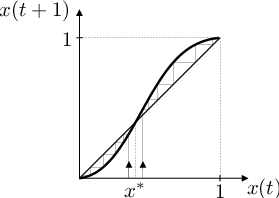
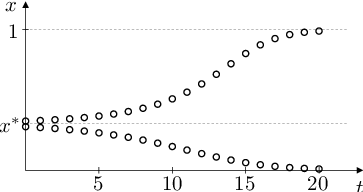
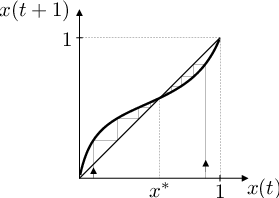
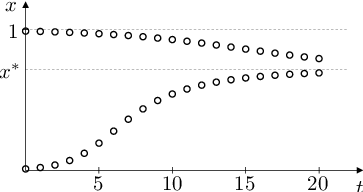
To znamená (viz obr. Aplikace 4), že pro každé řešení rovnice Aplikace (82) platí

Pokud výběr preferuje fenotyp určený recesivní alelou, pak dominantní alela z populace vymizí; pokud výběr preferuje fenotyp určený dominantní alelou, pak recesivní alela z populace vymizí.

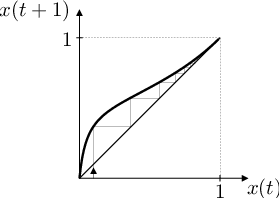
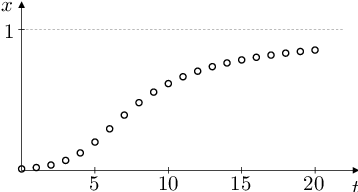
Obr. 4. Grafické řešení rovnice Aplikace (81) a jeho průběh pro různé hodnoty parametrů K, k. Tj. vývoj relativní frekvence alely A v populaci pro různé relativní reprodukční zdatnosti homozygotů vzhledem k heterozygotům.

(iii) každá alela nějak přispívá k reprodukční zdatnosti, žádná z nich není dominantní. Příspěvek alel k fenotypu je aditivní, alely jsou semidominantní.

I v tomto případě najdeme rovnovážné body rovnice Aplikace (81) a vyšetříme jejich stabilitu. Nyní označíme

Pak rovnice tj. kubická rovnice

má kořeny 0, 1 a Kořen je rovnovážným bodem rovnice Aplikace (82) pouze tehdy, když což nastane právě tehdy, když nebo (stále totiž předpokládáme ). Dále platí

To znamená (viz obr. Aplikace 4), že pro je rovnovážný bod 0 asymptoticky stabilní a pro je nestabilní. Podobně pro je rovnovážný bod 1 asymptoticky stabilní a pro je nestabilní. Pokud je rovnovážným bodem rovnice Aplikace (81), pak je asymptoticky stabilní v případě a nestabilní v případě ; snadno totiž ověříme, že při označení

platí pro a

což znamená, že

Podívejme se ještě na jeden speciální případ rovnice Aplikace (82), a to takový, když V tomto případě je

a to znamená, že reprodukční zdatnost heterozygota je geometrickým průměrem zdatností jednotlivých homozygotů. Rovnice Aplikace (82) nabude tvar

což je Bevertonova-Holtova rovnice, jejíž řešení je podle Riccatiho a Bernoulliova rovnice dáno formulí

Opět tedy platí

Je-li pak je možný genetický polymorfismus. Ten je ale v případě nestabilní; záleží na počáteční genetické struktuře populace, která z alel převládne. Trvalý genetický polymorfismus je možný jen v případě, že tj. reprodukční zdatnost každého z homozygotů je menší než reprodukční zdatnost heterozygota.

Z dosavadních úvah jsme vyloučili případ tj. možnost, že heterozygoti nejsou schopni reprodukce. V takovém případě má autonomní rovnice Aplikace (75) tvar

(83)

Pokud pak a alela by z populace vymizela hned v prvním časovém kroku. Takovou situaci bychom mohli interpretovat tak, že alela představovala nějakou škodlivou (smrtící) mutaci. Pokud pak a z populace by bezprostředně vymizela alela Dále budeme předpokládat tj. že ani alela ani alela nepředstavuje smrtící mutaci.

Konstantní posloupnosti a jsou evidentně řešením rovnice Aplikace (83) pro jakékoliv hodnoty parametrů vyjadřují možnost, že v modelované populaci má uvažovaný gen jedinou alelu. Budeme hledat další řešení rovnice Aplikace (83), které není identicky nulové ani jednotkové. Uvažujme proto rovnici spolu s počáteční podmínkou

(84)

Substituce

převede počáteční úlohu Aplikace (83), Aplikace (84) na počáteční úlohu pro lineární rovnici

která má řešení

Zpětnou substitucí dosatneme řešení původní počáteční úlohy Aplikace (83), Aplikace (84) ve tvaru

Posloupnost s obecným členem je vybraná z geometrické posloupnosti s počátečním členem a s kvocientem Hodnota kvocientu určuje chování řešení. Je-li

pak

a řešení úlohy Aplikace (83), Aplikace (84) je konstantní, Je-li resp. pak

přitom je řešení rovnice Aplikace (83) monotonní.

Pokud je tedy existuje rovnovážný stav který je repulsivní, a dva asymptoticky stabilní rovnovážné stavy 0 a 1. Ke kterému ze stabilních rovnovážných stavů bude řešení konvergovat, závisí na počáteční podmínce. Kvalitativně se tedy jedná o stejnou situaci jako na obr. Aplikace 4, případ

Závěr: Autonomní rovnice Aplikace (75) s nezápornými parametry uvažovaná na stavovém prostoru má rovnovážná řešení v krajních bodech tj. řešení a

Pokud jsou všechny parametry stejné, pak má rovnice pouze konstantní řešení; každý bod stavového prostoru je rovnovážný.

Pokud přičemž alespoň jedna z nerovností je ostrá, pak rovnice Aplikace (75) nemá uvnitř stavového prostoru   žádné rovnovážné body.

Pokud nebo pak má autonomní rovnice Aplikace (75) izolovaný rovnovážný bod

uvnitř stavového prostoru

Dostatečné podmínky pro asymptotickou stabilitu nebo repulsivitu izolovaných rovnovážných bodů jsou:

• Je-li nebo pak je stacionární řešení asymptoticky stabilní.
   
• Je-li nebo pak je stacionární řešení repulsivní.
   
• Je-li nebo pak je stacionární řešení asymptoticky stabilní.
   
• Je-li nebo pak je stacionární řešení repulsivní.
   
• Je-li pak je stacionární řešení asymptoticky stabilní.
   
• Je-li pak je stacionární řešení repulsivní.

Biologickou evoluci lze chápat jako změnu frekvencí alel v průběhu času. Představme si, že celá populace má na příslušném lokusu alelu a v počátečním čase se u nějakého jedince objeví její mutace, alela Pokud v takovém případě bude přičemž alespoň jedna z těchto nerovností je ostrá, pak se bude mutovaná alela v populaci šířit a nakonec v ní převládne; pokud pak budou obě alely v populaci dlouhodobě koexistovat, populace se stane geneticky polymorfní.