Riccatiho a Bernoulliova rovnice

Riccatiho diferenční rovnice je tvaru

(4)

kde je nenulová regresivní posloupnost. Rovnici můžeme přepsat ve tvaru rekurentní formule

(5)

nebo explicitní diferenční rovnice prvního typu

S využitím operátorů posunu a diference můžeme rovnici Některé explicitně řešitelné rovnice (4) přepsat do tvaru

a z něho vyjádřit diferenci hledané posloupnosti

Tato rovnice je diskrétní analogií Riccatiho diferenciální rovnice

Riccatiho diferenční rovnici řešíme pomocí substituce

(6)

Dosadíme do rekurentní formule Některé explicitně řešitelné rovnice (5) a postupně upravujeme:

Odtud vidíme, že posloupnost je řešením lineární homogenní diferenční rovnice druhého řádu

kterou můžeme také zapsat stručněji pomocí operátorů posunu a diference

Tvrzení 2.1. Riccatiho diferenční rovnice Některé explicitně řešitelné rovnice (4) pro neznámou posloupnost se substitucí Některé explicitně řešitelné rovnice (6) transformuje na lineární homogenní rovnici druhého řádu pro neznámou posloupnost

Příklad 2.2.

Zavedeme substituci

dosadíme do dané rovnice a postupně ji upravíme

Daná rovnice se tedy transformuje na lineární homogenní rovnici druhého řádu

Její charakteristická rovnice má dva reálné různé kořeny

Obecné řešení lineární diferenční rovnice tedy je

Označme Pro počáteční hodnoty dále platí a z toho vypočítáme

Z těchto podmínek dostaneme systém (algebraických) rovnic pro konstanty

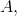
tj.

Z něho vypočítáme Řešení úlohy pro lineární rovnici je

Zpětnou substitucí tedy dostaneme řešení zadané úlohy ve tvaru

 

Pokud tj. na pravé straně rovnice Některé explicitně řešitelné rovnice (4) je nula, můžeme použít jednodušší substituci. V tomto případě položíme

(7)

dosadíme do rovnice Některé explicitně řešitelné rovnice (4) a vynásobíme výrazem Dostaneme

Je-li přitom posloupnost regresivní, upravíme tuto rovnici na tvar lineární diferenční rovnice prvního řádu

Tato rovnice má podle věty Lineární rovnice 2.5 řešení

kde Platí tedy:

Tvrzení 2.3. Je-li ak má Riccatiho rovnice řešení

Rovnice Některé explicitně řešitelné rovnice (4) s a s regresivní posloupností se v literatuře objevuje v rozmanitých tvarem. Ukážeme některé z nich. Rovnici v takovém případě můžeme přepsat na tvar

a při označení

dostaneme

neboli

(8)

případně

(9)

S pomocí operátoru posunu můžeme rovnici Některé explicitně řešitelné rovnice (8) přepsat ve tvaru

Vynásobením výrazem dostaneme rovnici ve tvaru

Z ní můžeme vyjádřit

nebo

(10)

Poslední rovnici vynásobíme jmenovatelem pravé strany a upravíme na tvar

ze kterého dostaneme jiné vyjádření diference hledané posloupnosti

Bernoulliova diferenční rovnice je tvaru

(11)

kde je nějaké reálné číslo. Bernoulliovu diferenční rovnici můžeme také vyjádřit ve tvaru rekurentní formule

Porovnáním s rovnicí Některé explicitně řešitelné rovnice (9) vidíme, že Riccatiho rovnice Některé explicitně řešitelné rovnice (4) s je speciálním případem Bernoulliovy rovnice Některé explicitně řešitelné rovnice (11) s parametrem

Tvar Bernoulliovy rovnice bezprostředně ukazuje, že substituce

(12)

transformuje Bernoulliovu diferenční rovnici Některé explicitně řešitelné rovnice (11) na lineární nehomogenní rovnici prvního řádu

(13)

Tvrzení 2.4.  Bernoulliova diferenční rovnice Některé explicitně řešitelné rovnice (11) pro neznámou posloupnost se substitucí Některé explicitně řešitelné rovnice (12) transformuje na lineární nehomogenní rovnici prvního řádu Některé explicitně řešitelné rovnice (13) pro neznámou posloupnost

Příklad 2.5. Bevertonovu-Holtovu rovnici Přípravné úvahy (16) můžeme přepsat ve tvaru

Jedná se tedy o rovnici Některé explicitně řešitelné rovnice (10), tj. rovnici, která je současně Riccatiho i Bernoulliova. Můžeme ji tedy vyřešit substitucí Některé explicitně řešitelné rovnice (12). Tato substituce byla v úvodu k této kapitole nalezena intuitivnějším způsobem.