Vícerozměrný dvouvýběrový t-test

Představme si, že máme dvě skupiny objektů či subjektů (např. pacienty se schizofrenií a zdravé subjekty), u nichž byly naměřeny hodnoty celé řady proměnných (např. objemy mozkových struktur, výsledky kognitivních testů apod.), a chtěli bychom zjistit, zda se tyto dvě skupiny od sebe liší. Srovnání těchto skupin podle každé proměnné zvlášť pomocí klasického jednorozměrného dvouvýběrového t-testu nám v tomto případě nestačí, protože bychom se na data nedívali globálně a mohly by nám tak uniknout některé souvislosti, vztahy atd. Vhodnou volbou je v tomto případě použití vícerozměrného dvouvýběrového t-testu.  

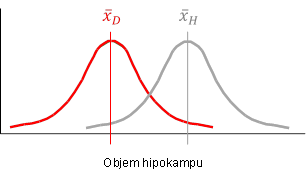
Při odvozování vícerozměrného dvouvýběrového t-testu začneme od stručného popisu jednorozměrného dvouvýběrového t-testu. Cílem jednorozměrného dvouvýběrového t-testu je srovnání dvou skupin dat popsaných jednou proměnnou, přičemž skupiny jsou na sobě nezávislé, tedy mezi objekty neexistuje vazba (Obr. 1). Předpokladem tohoto testu je normalita dat v obou skupinách a shodnost (homogenita) rozptylů ve skupinách.

Testová statistika jednorozměrného dvouvýběrového t-testu je  , kde  je Studentovo t rozdělení pravděpodobnosti s  stupni volnosti,  a  jsou výběrové průměry hodnot dané proměnné u pacientů a kontrol,  je vážený rozptyl vypočtený jako , přičemž  a   jsou rozptyly dané proměnné u pacientů a kontrol, a c je konstanta, o kterou se má rozdíl průměrů lišit (zpravidla ). Nulová hypotéza o shodě středních hodnot  je zamítnuta, pokud .

Využijeme nyní toho, že jednorozměrný dvouvýběrový t-test se statistikou T je ekvivalentní testu

(1)

kde , tedy  se řídí Fisherovým F rozdělením pravděpodobnosti se stupni volnosti 1 a . Nulová hypotéza o shodě středních hodnot  je zamítnuta v případě, že .

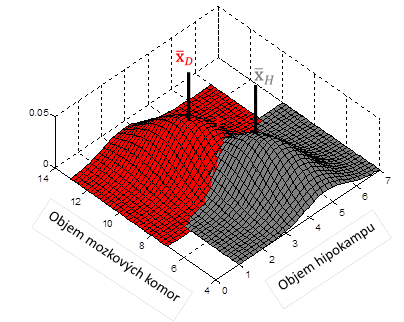
Jak už bylo naznačeno výše, vícerozměrný dvouvýběrový t-test použijeme v případě, že chceme srovnat dvě skupiny dat, které jsou popsány více proměnnými (Obr. 2). Při odvození vícerozměrného dvouvýběrového t-testu vyjdeme ze vztahu (1), přičemž výběrové průměry a  nahradíme za vektory výběrových průměrů  a  a vážený rozptyl  nahradíme za váženou kovarianční matici , kde  a  jsou výběrové kovarianční matice pacientů a kontrol. Získáváme tak dvouvýběrovou Hotellingovu  testovou statistiku

(2)

kde c je vektor konstant, o kterou se mají rozdíly vektorů výběrových průměrů lišit (zpravidla nulový vektor) a  má Hotellingovo rozdělení s parametry , , kde . Předpoklady jsou analogické jako při použití jednorozměrného dvouvýběrového t-testu, tedy předpokladem je vícerozměrná normalita dat v obou skupinách a shodnost kovariančních matic.

Hotellingovu  testovou statistiku můžeme transformovat na F statistiku se stejnými parametry jako testová statistika  pomocí

(3)

Nulová hypotéza o shodě vektorů středních hodnot  je zamítnuta, pokud , což je vnější část p-rozměrného elipsoidu se středem v   . Pokud by sestrojený elipsoid obsahoval bod daný vektorem c (pokud je c nulový vektor, jedná se o počátek souřadnic), nezamítáme nulovou hypotézu o shodě vektorů středních hodnot. V opačném případě (tzn., leží-li bod c mimo elipsoid), zamítáme nulovou hypotézu.

Poznámka: Analogickým způsobem je možné odvodit vícerozměrný párový t-test z jednorozměrného párového t-testu.