Wardova metoda

Je kombinovaný postup, který potřebuje jak znalost všech vektorů obou uvažovaných množin, tak i znalost reprezentativních vektorů. Vzdálenost mezi množinami je podle této metody definována přírůstkem součtu čtverců odchylek mezi centroidem a vektory množiny vytvořené z obou vstupních množin a oproti součtu čtverců odchylek mezi vektory a centroidy v obou množinách a .

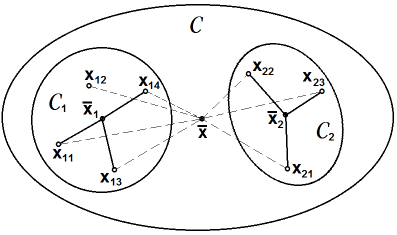
Jsou-li  a  n-rozměrné centroidy množin a a centroid sjednocené množiny, pak je Wardova metrika definována výrazem (viz Obr.9)

Wardova metoda vytváří vztah mezi rozptyly celé množiny vektorů a rozptyly v obou dílčích množinách. Má tendenci vytvářet kompaktní, poměrně malé množiny, zhruba stejné velikosti.

Příklad 7.8

Předpokládejme opět vektory vektory  = (0, 0), = (10, 10),  = (8, 8),  = (6, 7),  = (4, 3) a  = (3, 2) rozdělené do dvou množin = {x₁, x₅, x₆} a = {x₂, x₃, x₄}. Jaká je vzdálenost obou množin Wardovy metody?

Řešení:

Souřadnice centroidu množiny jsou dány středními hodnotami souřadnic všech vektorů z této množiny, tj. stejně jako v příkladu 7.7   a  a celkového centroidu .

Výpočet Wardovy vzdálenosti pak vede k hodnotě