Nelineární verze metody podpůrných vektorů

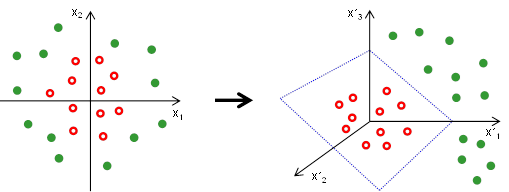
Metoda podpůrných vektorů, jak jsme si dosud ukazovali, sloužila k oddělení dvou skupin objektů (či subjektů) pomocí lineární hranice. V praxi však může nastat situace, kdy by pro oddělení skupin objektů bylo vhodnější použít nelineární hranici (např. Obr. 12 vlevo). V takovém případě se jeví jako vhodné transformovat data do nového prostoru (zpravidla o vyšší dimenzi než původní prostor), ve kterém bude možné objekty oddělit lineárně (viz. Obr. 12 vpravo). Abychom toho dosáhli, můžeme při vytváření klasifikátoru použít místo p původních proměnných i jejich kvadratické či kubické formy, tedy vstupem do klasifikátoru budou např. proměnné . Takovéto rozšíření původního počtu proměnných pak umožní, že v prostoru, který bude mít nyní dimenzí, budou data lineárně separabilní. Místo polynomiálních členů můžeme samozřejmě použít jakékoliv jiné funkce v závislosti na typu dat. Musíme však mít na paměti, že přidání jakýchkoliv takovýchto členů může mnohonásobně zvýšit počet proměnných, takže pak budou výpočty velmi náročné. Metoda podpůrných vektorů (konkrétně její nelineární verze) však umí řešit takovéto navýšení počtu proměnných elegantním způsobem, takže se výpočetní náročnost příliš nezvyšuje.

Nelineární verze metody podpůrných vektorů totiž transformuje prostor specifickým způsobem, a to pomocí tzv. jader (kernels). U lineární metody podpůrných vektorů pro lineárně separabilní i neseparabilní třídy jsme si ukázali, že je možné upravit klasifikátor do podoby (26) resp. (40), přičemž skalární součin  si můžeme zapsat obecně jako , kde  je nějaká funkce, kterou nazveme jádro. Pokud

(41)

jedná se o lineární jádro a výsledným klasifikátorem je tedy lineární verze metody podpůrných vektorů. Můžeme ale volit i jiná jádra, která vedou k nelineární klasifikaci dat:

• polynomiální jádro stupně d: ,
• radiální bázové jádro: ,
• atd.

Tato jádra nám umožní transformovat data do prostoru o vyšší dimenzi tím, že jsou počítány polynomiály stupně apod. Na rozdíl od situace, kdy bychom pouze přidali mocniny původních proměnných a provedli lineární verzi metody podpůrných vektorů, se však v tomto případě při použití jader výpočetní náročnost příliš nezvýší, protože ve skutečnosti nemusíme klasifikaci provádět v prostoru o vyšší dimenzi, pouze počítáme složitější jádro. Navíc u metody podpůrných vektorů (ať už její lineární či nelineární verze) je úspora výpočetní náročnosti i v tom, že mnoho členů z výrazu (26) resp. (40) je nulových, protože  je nulové pro všechny objekty (resp. subjekty), které nejsou podpůrnými vektory.