
Úvod do klasifikace dat pomocí diskriminačních funkcí
V předchozí kapitole jsme si uvedli, že diskriminační funkce jsou jednou z možností, jak vymezit klasifikační třídy v -rozměrném prostoru. Diskriminační funkce
vyjadřují míru příslušnosti objektu
do jednotlivých tříd
. Objekt
zařadíme do takové třídy
, pro niž je
maximální. Ukázkový příklad pro dichotomický klasifikátor (tzn. klasifikace do dvou tříd) je uveden na Obr. 1. Na základě diskriminačních funkcí zařadíme neznámý objekt do třídy
, protože
.
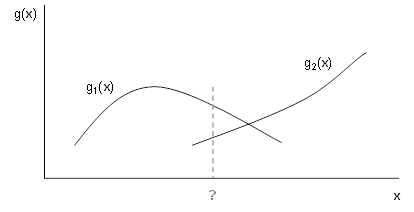
Obr. 1: Ilustrace klasifikace pomocí diskriminačních funkcí. Neznámý objekt (označený otazníkem) zatřídíme do , protože
.
Dichotomický klasifikátor můžeme znázornit pomocí blokového schématu na Obr. 2. Pro daný objekt , který chceme klasifikovat, přivedeme současně všechny hodnoty jednotlivých proměnných (tzn.
) do K=2 bloků, ve kterých se vyčíslí hodnoty diskriminačních funkcí
a
. Na výstupu výběrového bloku se objeví identifikátor té klasifikační třídy
, pro niž byla hodnota diskriminační funkce větší.
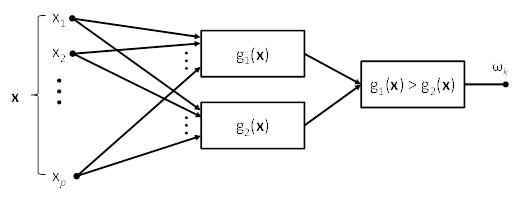
V případě dichotomického klasifikátoru lze rozhodovací pravidlo zapsat rovněž ve tvaru:
|
|
(1)
|
kdy zařadíme objekt do třídy
, pokud
. V případě, že
, zařadíme objekt
do třídy
. Pokud je
a nemůžeme tedy jednoznačně rozhodnout, kam máme objekt
zařadit, přiřadíme ho náhodně do jedné ze skupin, případně ho zařadíme do rizikovější skupiny. Například subjekt s ne zcela průkazným podezřením na infarkt myokardu raději zařadíme do skupiny pacientů, abychom ho nechali na pozorování v nemocnici, než bychom ho označili za zdravého a poslali domů, kde by mohl zemřít.
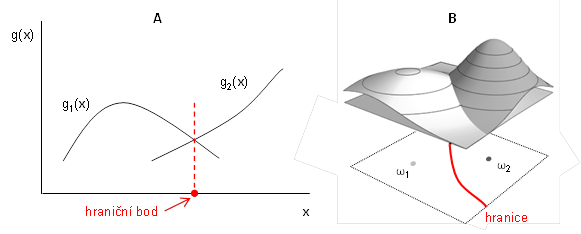
V případě, že , pak i
, což znamená, že se diskriminační funkce protínají. Průmět průsečíku diskriminačních funkcí nám určuje hranici mezi třídami. Existuje tu tedy souvislost klasifikace podle diskriminačních funkcí s klasifikací pomocí hranic. Ukázky pro klasifikaci pomocí jedné a dvou proměnných jsou uvedeny na Obr. 3. Pokud bude objekt či subjekt, kterého chceme klasifikovat, ležet vlevo od hraničního bodu (v případě A) nebo vlevo od hranice (v případě B), zařadíme ho do třídy
, což je ekvivalentní tomu, že vlevo od hraničního bodu resp. hranice je
.
Po vysvětlení principu klasifikace pomocí diskriminačních funkcí a její souvislosti s klasifikací pomocí hranic, si uvedeme příklady diskriminačních funkcí. Nejjednodušším tvarem diskriminační funkce je lineární diskriminační funkce:
|
|
(2)
|
kde je práh diskriminační funkce posouvající počátek souřadného systému a
jsou váhové koeficienty i-té proměnné
. Ukázka klasifikace pomocí lineárních diskriminačních funkcí je na Obr. 4.
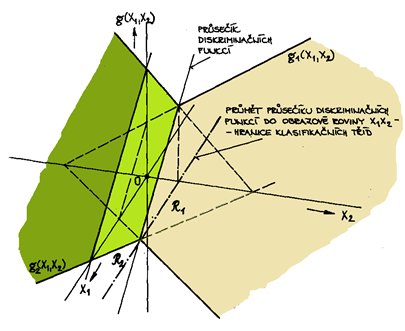
Obr. 4. Ukázka klasifikace pomocí lineárních diskriminačních funkcí.
Dalším příkladem diskriminačních funkcí jsou funkce založené na statistických vlastnostech třídy objektů. Konkrétně se budeme věnovat Bayesovu klasifikátoru, který zařazuje objekty do tříd podle podmíněné pravděpodobnosti zatřídění objektu do daných tříd. Bayesův klasifikátor si detailněji popíšeme v následujících podkapitolách, které jsou rozděleny podle kritéria použitého při vytváření klasifikátoru:
- kritérium maximální aposteriorní pravděpodobnosti,
- kritérium minimální pravděpodobnosti chybného rozhodnutí,
- kritérium minimální střední ztráty,
- kritérium maximální pravděpodobnosti.




