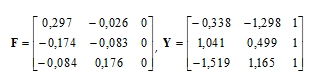Požadavky na data a omezení korespondenční analýzy
Korespondenční analýza se používá ke zpracování kontingenčních tabulek, které obsahují pouze pozitivní hodnoty nebo nuly. Pouze pro takovou kontingenční tabulku lze určit podmíněné pravděpodobnosti. Korespondenční analýza nemůže být použita na data obsahující negativní hodnoty, data proto nesmí být centrována nebo standardizována.
Kontingenční tabulka nesmí obsahovat řádek s celkovým součtem nula ani sloupec s celkovým součtem nula.
Korespondenční analýza je citlivá na odlehlé hodnoty.
Data by měla být dimenzionálně homogenní, proměnné by měly být měřeny ve stejných jednotkách. Pouze v takovém případě je smysluplné hodnotit vzdálenosti mezi řádky a mezi sloupci matice. Při řádových rozdílech hodnot vstupní matice se doporučuje logaritmická transformace.
Problémem korespondenční analýzy může být tzv. obloukový efekt, který je možné odstranit pomocí detrendované korespondenční analýzy (detrended correspondence analysis, DCA).
Příklad 1
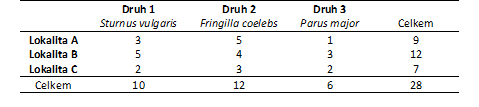
Korespondenční analýza se používá zejména ke zpřehlednění rozsáhlých kontingenčních tabulek obsahujících mnohočetné kategorie. Kvůli přehlednosti a názornosti výpočtů zde uvádíme příklad třech ptačích druhů zaznamenaných na třech lokalitách. První proměnná je tvořena třemi kategoriemi - lokalita A, B, C a druhá proměnná také třemi kategoriemi - Sturnus vulgaris, Fringilla coelebs, Parus major (Tabulka 1, Obr. 1). Hodnoty v tabulce označují počet zaznamenaných hnízdících párů, které současně náleží do příslušné řádkové a sloupcové kategorie.
Tabulka 1: Zastoupení třech druhů ptáků na třech lokalitách.
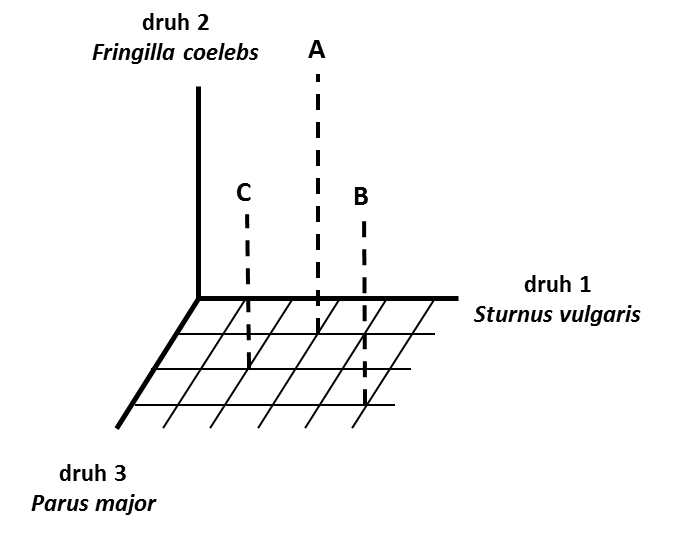 |
Obr.1: Umístění lokalit (A, B, C) v prostoru tvořeném třemi ptačími druhy.
Korespondenční matice z dat v Tabulce 1 je pak:
 |
Vektory řádkových a sloupcových zátěží jsou
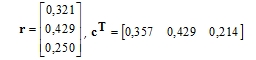 |
Inverzní matice k diagonálním maticím řádkových a sloupcových profilů jsou
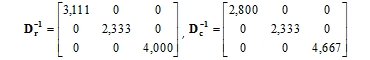 |
Řádkové a sloupcové profily jsou pak
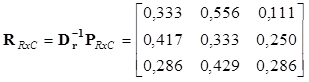 |
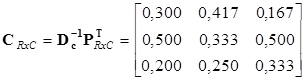 |
Podle vzorce (11) vypočteme chí-kvadrát vzdálenosti mezi řádky v našem příkladu. Chí-kvadrát vzdálenost mezi prvním a druhým řádkem (lokalita A, lokalita B) je:
Podobně vypočteme vzdálenost pro ostatní kombinace řádkových profilů a sloupcových profilů a uvedeme je v tabulkách 2 a 3.
Tabulka 2: Chí-kvadrát vzdálenosti řádkových profilů.
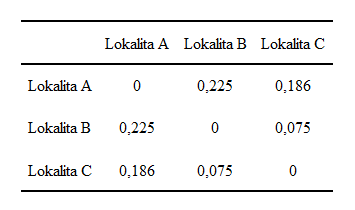
Tabulka 3: Chí-kvadrát vzdálenosti sloupcových profilů.
.png)
Na datech z našeho příkladu provedeme rozklad korespondenční matice pomocí zobecněné singulární dekompozice. Podle vzorce (12) je matice standardizovaných reziduí
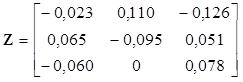 |
Rozklad na singulární hodnoty podle vzorce (14) je pak:
 |
Z matice singulárních hodnot určíme vlastní čísla matice jako čtverec singulárních hodnot: ,
.
Souřadnice bodů vycházející ze sloupcové standardizace pak vypočteme podle (17) a (18).
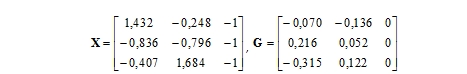 |
Souřadnice bodů vycházející ze simultánní standardizace obou kategorií jsou:
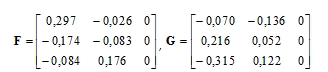 |
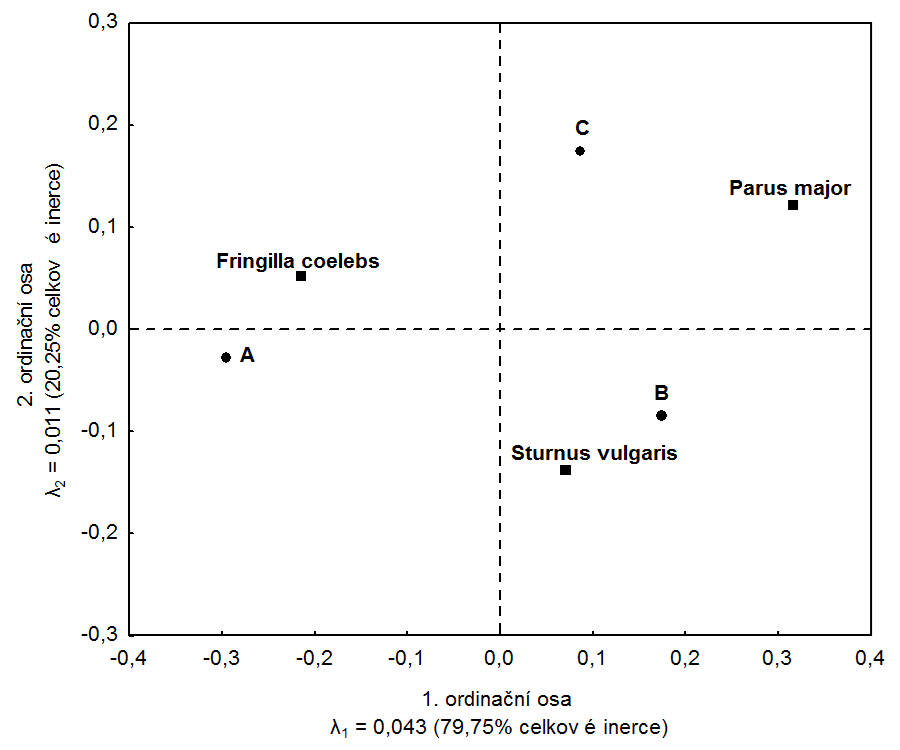 |
Obr. 2: Korespondenční mapa řádkových a sloupcových profilů. (Korespondenční analýza byla provedena a korespondenční mapa vykreslena v programu Statistica. Je zřejmé, že pozice druhů a lokalit souhlasí s vypočtenými hodnotami souřadnic v matici F a G
V korespondenční mapě jsou řádky i sloupce původní matice (v našem případě druhy a vzorky, Obr. 2) znázorněny body. Pozice druhů v korespondenční mapě představuje jeho optimum vzhledem k ordinačním osám. V případě analýzy ekologických dat jsou ordinační osy často interpretovány jako tzv. environmentální gradienty. Ty je možné definovat na základě znalostí o lokalitách zobrazených v korespondenční mapě. Korespondenční analýza předpokládá unimodální závislost druhů na gradientu tvořeném ordinačními osami.
V korespondenční mapě z výše uvedeného vyplývá:
- vzorky, které mají podobné druhové složení, budou v korespondenční mapě umístěny poblíž sebe;
- vzorky, které nemají společné druhy, budou v korespondenční mapě umístěny dále od sebe;
- druhy, které se vyskytovaly spolu ve vzorcích, budou v korespondenční mapě umístěny poblíž sebe;
- druhy, které se vyskytovaly v jiných vzorcích, budou v korespondenční mapě umístěny dále od sebe;
- druhy umístěny poblíž vzorků byly pro tyto vzorky typické, resp. se vyskytovaly pouze v nich;
- když se druh v daném vzorku nevyskytoval, budou od sebe v korespondenční mapě vzdáleny.
V našem příkladu se snažíme odhalit vztahy mezi ptačími druhy a lokalitami. Z korespondenční mapy (Obr. 2) vidíme, které druhy korespondují s konkrétními lokalitami. V korespondenční mapě je zřejmá vazba druhu Fringilla coelebs k lokalitě A a také druhu Sturnus vulgaris k lokalitě B. Uvedené druhy byly na těchto lokalitách nejpočetnější. Různé softwary škálují souřadnice řádkových a sloupcových kategorií různě, zachovávají ovšem vzájemné vztahy mezi kategoriemi, a tak neovlivňují interpretaci výsledku.
Vraťme se k našemu příkladu třech ptačích druhů zaznamenaných na třech lokalitách, na kterém ukážeme princip váženého průměrování. Pro lokality A, B, C zvolíme počáteční skóre lokalit, např. 1, 2, 3 (Tabulka 4). Výpočet skóre druhů jako vážený průměr skóre lokalit je pak:
Sturnus vulgaris:
Fringilla coelebs:
Parus major:
Po přeškálování na rozpětí 1-100 dostaneme hodnoty:
Sturnus vulgaris:
Fringilla coelebs:
Parus major:
Dále postupujeme výpočtem skóre lokalit WA1 jako vážených průměrů přeškálovaných skóre druhů: Lokalita A: (3⋅20,8+5⋅1+1⋅100)/9=18,6 , atd. Po tomto kroku znovu následuje přeškálování skóre lokalit. Vypočítané skóre jsou pak použity pro výpočet skóre druhů (WA2) jako vážených průměrů skóre lokalit, atd. Postupný výpočet je uvedený v tabulce 4. Výpočet můžeme ukončit, když se hodnoty výrazně neliší od výpočtu v předešlém cyklu; v našem případě jsme ukončili algoritmus po šesté iteraci.
Tabulka 4: Ukázka výpočtu první osy korespondenční analýzy metodou váženého průměrování na příkladu třech společenstev (A, B, C). Poč. skóre - počáteční náhodně zvolené skóre lokalit. WA 1 – WA 5 – skóre druhů/lokalit vypočítané jako vážený průměr ze skóre lokalit/druhů. Resc. – přeškálování na rozpětí 1–100.
.png)
Výsledek váženého průměrování můžeme opticky porovnat s korespondenční mapou na Obr. 2. Vidíme, že jak rozmístění lokalit, tak i umístění druhů na první ordinační ose souhlasí.
Dále pokračujeme v našem příkladu výpočtem celkové inerce . Spočítáme inerci sloupcových a řádkových kategorií, tím určíme příspěvek jednotlivých kategorií k celkové inerci. V sloupci Inerce tabulky 5 jsou řádkové inerce pro každou řádkovou kategorii vypočítané následovně:
Lokalita A: .
Ve sloupci Příspěvek bodu k inerci jsou příspěvky řádkových bodů k inerci v odpovídajícím rozměru. Příspěvek Lokality A k inerci první osy je: a k inerci druhé osy:
.
Obdobně dostaneme inerci a příspěvky bodů k inerci první a druhé osy pro ostatní řádkové kategorie.
Tabulka 5: Výsledky korespondenční analýzy třech ptačích druhů na třech lokalitách. Řádkové zátěže, souřadnice řádkových kategorií v prostoru prvních dvou os korespondenční analýzy, celková řádková inerce.
.png)
Podobně, jak tomu bylo u řádkových kategorií, jsou spočítány sloupcové inerce a příspěvky sloupcových bodů k inerci v odpovídajícím rozměru v tabulce 6.
Tabulka 6: Výsledky korespondenční analýzy třech ptačích druhů na třech lokalitách. Sloupcové zátěže, souřadnice sloupcových kategorií v prostoru prvních dvou os korespondenční analýzy, celková sloupcová inerce.
.png)
Příklad 2
Interpretujte výsledky korespondenční analýzy podle tab. 7, 8, 9, 10 a Obr. 3.
Data pocházejí z monitoringu drobných zemních savců (DZS) v alpínském pásmu NP Nízké Tatry. Sledované území představovaly tři plochy označené HP - hlavní plocha, VP - vedlejší plocha, OB - okolí budovy. Plochy byly tvořeny zejména sutinami a skalními poli, z rostlinného společenstva převládá společenstvo Juncetea trifidi. Hlavní a vedlejší plocha se od sebe lišila zejména poměrem skalních polí a rostlinného porostu. Na hlavní ploše převládalo rostlinné společenstvo, na vedlejší skalní pole. Třetí plochu tvořilo okolí budovy televizního vysílače, prostředí této plochy tvořil zejména travnatý porost a štěrk.
Sledování DZS probíhalo v roce 2005 a 2006. Tyto roky se lišily klimatickými podmínkami, rok 2005 byl nepříznivější, což se odrazilo na počtu zaznamenaných jedinců. Celkem bylo zaznamenáno šest druhů savců: Chionomys nivalis (Ch.n.), Clethrionomys glareolus (C.g.), Microtus tatricus (M.t.), Microtus agrestis (M.agr.), Apodemus flavicollis (A.f.), Sorex araneus (S.a.).
Tabulka 7: Zastoupení šesti druhů drobných zemních savců (DZS) na třech lokalitách ve dvou letech. Význam zkratek je v textu příkladu (Nepublikovaná data I. Čornaninová).
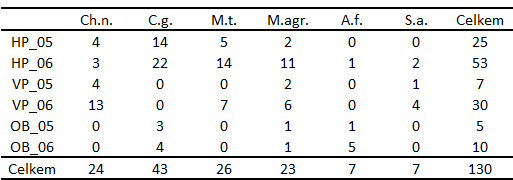
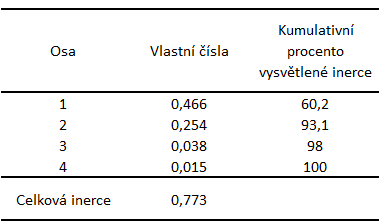
Tabulka 8: Výsledek korespondenční analýzy šesti druhů DZS na třech lokalitách ve dvou letech (tab. 7).
 |
Obr. 3: Korespondenční mapa. Výsledek korespondenční analýzy šesti druhů DZS na třech lokalitách ve dvou letech. Význam zkratek je uveden v textu příkladu.
Tabulka 9: Výsledky korespondenční analýzy šesti druhů DZS na třech lokalitách ve dvou letech. Řádkové zátěže, souřadnice řádkových kategorií v prostoru prvních dvou os korespondenční analýzy, celková řádková inerce. Význam zkratek je uveden v textu příkladu.
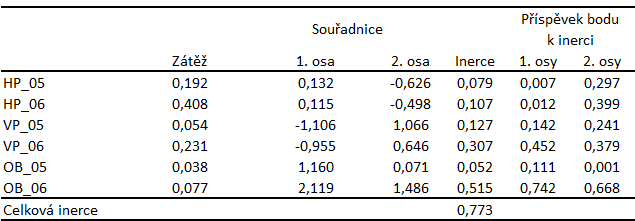
Tabulka 10: Výsledky korespondenční analýzy šesti druhů DZS na třech lokalitách ve dvou letech. Sloupcové zátěže, souřadnice sloupcových kategorií v prostoru prvních dvou os korespondenční analýzy, celková sloupcová inerce. Význam zkratek je uveden v textu příkladu.
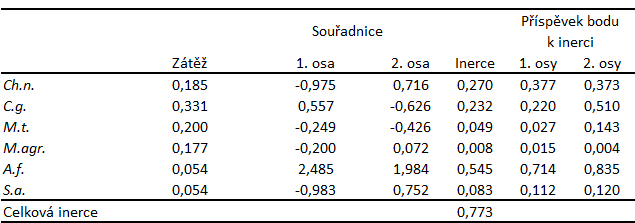
Z číselných výsledků v tabulce 8 je zřejmé, že první dvě osy korespondenční mapy vysvětlují 93,1% inerce korespondenční tabulky. Toto je dostatečně vysoká hodnota, a tak můžeme přistoupit k interpretaci výsledků. Podle rozmístění bodů řádkových a sloupcových kategorií na korespondenční mapě (Obr. 3) je zjevné symetrické zobrazení řádkových a sloupcových kategorií. Proto nemůžeme uvažovat vztahy mezi druhy a plochami na základě konkrétních vzdáleností mezi zobrazenými body. A tak přistoupíme k interpretaci ordinačních os na základě rozmístění řádkových bodů - ploch a definujeme smysl ordinačních os. Pak interpretujeme vztah druhů k prostředí na základě rozmístění sloupcových kategorií v korespondenční mapě. V některých případech může být vhodnější interpretovat kvadranty korespondenční mapy.
Smysl první osy bychom mohli definovat jako přechod od prostředí s vyšším podílem skalních polí k prostředí s vyšším podílem rostlinných porostů. Charakterizace druhé osy je poněkud obtížnější, pravděpodobně souvisí se strukturální rozmanitostí jednotlivých ploch - od nejrozmanitější hlavní plochy, přes méně diverzifikovanou vedlejší plochu až po plochu v okolí budovy, které prostředí bylo nejvíce jednotvárné (Obr. 3, Tab. 9).
Pro výskyt druhu Chionomys nivalis je nejdůležitější vysoký podíl skal v prostředí. Podobné prostředí vyhovuje i druhu Sorex araneus. Druhy Clethrionomys glareolus, Microtus tatricus, a Microtus agrestis obývají prostředí s menším zastoupením skal a vyšším podílem rostlinných společenstev, prostředí které je strukturálně dostatečně heterogenní. Druh Apodemus flavicollis byl zaznamenán především na ploše v okolí budovy, která danému druhu zřejmě poskytovala vhodné krycí i potravní možnosti (Obr. 3, Tab. 10).