Hierarchické aglomerativní shlukování

Aglomerativní shluková analýza pracuje se samostatnými objekty, které jsou shlukovány do větších shluků. V mnohých vědních disciplínách jsou aglomerativní techniky používány častěji než divizivní metody. Existuje mnoho aglomerativních metod, přičemž každá z nich využívá jiný pohled na data.

Základním krokem tohoto shlukování je výpočet podobností/vzdáleností mezi všemi dvojicemi objektů, tj. vytvoření asociační matice. V různých etapách algoritmu posuzujeme podobnost/vzdálenost dvou objektů, podobnost/vzdálenost objektu a shluku a podobnost/vzdálenost dvou shluků. Způsob výpočtu podobnosti/vzdálenosti zásadním způsobem ovlivňuje výsledek shlukování.

V kapitole Podobnosti a vzdálenosti ve vícerozměrném prostoru  jsou uvedeny různé míry podobnosti a metriky vzdálenosti. Většinou požadujeme, aby podobnost nabývala hodnot od nuly pro maximální rozdílnost po jedničku pro totožnost. Často se však místo podobností používají z praktických důvodů různé míry vzdálenosti, tentýž jev je tedy měřen v opačném směru. Nevyplývají z toho žádné problémy; ostatně každou míru vzdálenosti lze převést na míru podobnosti , , např. a naopak.

Obecný postup aglomerativního hierarchického shlukování je následující:

1. Vypočteme asociační matici vhodných měr vzdálenosti/podobnosti.
2. Proces začneme od rozkladu , tj. od n shluků, z nichž každý obsahuje jeden objekt.
3. V asociační matici najdeme dva objekty/shluky (-tý a -tý), jejichž vzdálenost je minimální (resp. podobnost je maximální).
4. Spojíme dva objekty/shluky nalezené v bodě 3 (-tý a -tý) do nového shluku (-tý). V původní matici vymažeme -tý a -tý řádek i sloupec a nahradíme je řádkem i sloupcem pro nový shluk. V tomto novém řádku a sloupci je vzdálenost ke všem původním shlukům vypočítána vhodným způsobem hodnocení vzdálenosti mezi shluky. Řád matice se sníží o jednu.
5. Zaznamenáme pořadí cyklu rozkladu , dále identifikaci spojených objektů/shluků , a hladinu pro spojení .
6. Pokud proces vytváření rozkladů již neskončil spojením všech objektů do jediného shluku , pokračujeme znovu bodem 3.

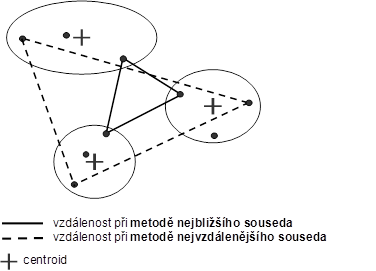
Výsledky hierarchického aglomerativního shlukování se budou lišit podle způsobu, jakým hodnotíme vzdálenosti mezi shluky. V dalším textu stručně doplníme poznatky o vzdálenosti mezi shluky. Způsob vnímání vzdálenosti mezi shluky se označuje také pojmy aglomerativní metoda, aglomerativní postup, nebo shlukovací algoritmus (Obr. 2).

Obr.2: Vnímání vzdálenosti při metodě nejbližšího a nejvzdálenějšího souseda.

Metoda nejbližšího souseda. Při použití této metody se často i značně vzdálené objekty mohou sejít ve stejném shluku, pokud větší počet dalších objektů mezi nimi vytvoří jakýsi most (Obr. 3a). Toto charakteristické řetězení objektů se považuje za nevýhodu, zvláště když máme důvod požadovat, aby shluky měly obvyklý eliptický tvar se zhutněným jádrem.

Metoda nejvzdálenějšího souseda. Tato metoda produkuje shluky, které jsou mezi sebou dobře odděleny (Obr. 3b). Nežádoucí řetězový efekt zde odpadá, naopak je tu tendence ke tvorbě kompaktních shluků, které nebývají velké.

Metoda průměrné vazby vede často k podobným výsledkům jako metoda nejvzdálenějšího souseda.

Centroidová metoda již nevychází ze shrnování informací o mezishlukových vzdálenostech objektů. Kritérium je vzdálenost centroidů. Při této metodě je vzdálenost mezi shluky počítána jako vzdálenost mezi centroidy těchto shluků. Nevýhodou centroidové metody je skutečnost, že v případě spojování dvou shluků velmi rozdílné velikosti bude centroid nového shluku velmi blízko většího shluku (nebo dokonce uvnitř). Vlastnosti menšího shluku se tak do jisté míry ztrácejí. (Obr. 3c)

Wardova metoda je podobná metodě průměrné vazby a centroidové metodě (Obr. 3d). Má tendenci odstraňovat malé shluky, tedy tvořit shluky zhruba shodné velikosti, což je často vítaná vlastnost.

Obr. 3: Ukázka dendrogramu vzniklého metodou nejbližšího souseda (a), metodou nejvzdálenějšího souseda (b), centroidovou metodou (c) a Wardovou metodou (d) a pozice původních dat v dvourozměrném prostoru (podle [11], doplněno).
 

Příklad 1
Interpretaci výsledku hierarchického aglomerativního shlukování si představíme na konkrétním příkladu. Cílem bylo zjistit podobnost šesti lokalit ve třech časových obdobích z hlediska výskytu korýšů. Zajímalo nás, jestli si jsou lokality podobnější v čase nebo v prostoru. Vstupní matici tvořilo 63 taxonů korýšů vyskytujících se v 18 objektech. Objekty představovalo šest lokalit v záplavové oblasti Dunaje ve třech obdobích (1: 1991–1992 před přehrazením Dunaje, 2: 1993–1997 prvních 5 let po přehrazení, 3: 1999–2004 dalších 6 let po přehrazení). Sledovanými lokalitami byly: D: Dobrohošť, G: Gabčíkovo, B: Bodíky, I: Istragov, K: Kráľovská lúka, S: Sporná sihoť. Početnost jednotlivých taxonů korýšů byl kvantifikován na desetistupňové škále. Charakter dat umožnil použití euklidovské vzdálenosti. Vzdálenost mezi shluky byla určena metodou nevzdálenějšího souseda. Výpočet byl proveden v softwaru Statistica. Další možností je použití softwaru SYN-TAX.

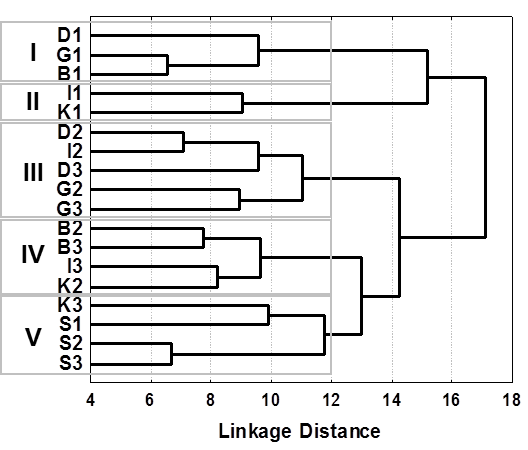Obr. 4: Ukázka výsledku shlukové analýzy společenstev korýšů (podle [5]).

Interpretace dendrogramu je následující (Obr. 4): na určené hladině spojování 12 (linkage distance) se vytvořilo pět shluků lokalit. Tuto hladinu spojování, na které jsme interpretovaly vzniklé shluky, jsme určily expertním odhadem na základě naší znalosti stavu sledovaných lokalit a jejich společenstev korýšů. První shluk (I) obsahuje lokality D1, G1, B1 – lokality Dobrohošť, Bodíky a Gabčíkovo před přehrazením Dunaje. V tomto shluku jsou si nejpodobnější lokality Gabčíkovo a Bodíky (jsou sloučeny na nižší hladině spojování). Druhý shluk (II) obsahuje lokality I1, K1 (tzn. Istragov a Kráľovská lúka v období před přehrazením). Třetí shluk obsahuje lokality D2, D3, G2, G3, I2 (tzn. Dobrohošť a Gabčíkovo ve druhém a třetím období společně s lokalitou Istragov ve druhém období). V tomto shluku jsou si nejpodobnější lokality Dobrohošť ve druhém období a Istragov taky ve druhém období. Čtvrtý shluk je tvořený lokalitami B2, B3, I3, K2 (tzn. Bodíky ve druhém a třetím období, Istragov ve třetím období a Kráľovská lúka ve druhém období). Poslední pátý shluk je tvořen lokalitami K3, S1, S2, S3 (tzn. Sporná sihoť ve všech obdobích a Kráľovská lúka ve třetím období).

Je velmi žádoucí doplnit takové zhodnocení dendrogramu o popis, co mají dané objekty - v tomto případě lokality v časových obdobích - v jednotlivých shlucích společné a čím se shluky mezi sebou liší. Můžeme uvažovat společný výskyt konkrétních taxonů v jednom shluku a absence jiných taxonů přítomných v jiném shluku apod. K tomu je vhodné seřadit původní datovou tabulku a najít skupiny taxonů typických pro jednotlivé shluky (Tabulka 1). Interpretaci dendrogramu v našem příkladě můžeme teda doplnit o následovná konstatování. Pro shluky I a II je typický druh Moina brachiata, který se v ostatních shlucích nevyskytoval. Dále v těchto dvou shlucích chybí druhy Daphnia galeata, Diaphanosoma orghidani, Disparalona rostrata Macrothrix hirsuticornis, které jsou přítomny ve všech ostatních shlucích. Shluk I se dále vyznačuje nepřítomností druhů Alona rectangula, Pleuroxus aduncus, Sida crystallina, přítomných ve všech ostatních shlucích. Pro třetí shluk jsou typické druhy Ilyocryptus sordidus a Leydigia leydigii, pro čtvrtý druhy Pleuroxus laevis, Pseudochydorus globosus a pro pátý druhy Acroperus neglectus, Ceriodaphnia quadrangula, Ceriodaphnia reticulata. Čtvrtý a pátý shluk jsou si blízké společnou přítomností druhů Alonella nana, Ceriodaphnia megops, Pleuroxus truncatus, Simocephalus serrulatus.

Tabulka 1: Část vstupní tabulky výskytu korýšů na šesti lokalitách ve třech obdobích. Z celkového počtu 63 taxonů je v tabulce uvedeno pouze 19, které se zdají být vhodné k interpretaci shluků vytvořených aglomerativním shlukováním. Druhy i lokality jsou vhodně seřazeny pro lepší interpretaci dendrogramu (Obr. 4).

Podle umístění jednotlivých lokalit v shlucích můžeme konstatovat, že první období před přehrazením Dunaje bylo zcela odlišné od dalších dvou časových období. V dalších dvou sledovaných časových obdobích je zřejmá spíše prostorová podobnost společenstev korýšů než-li časová.

Na Obr. 5 lze vidět, jak různé jsou výsledné dendrogramy při použití různých měr vzdálenosti mezi shluky.

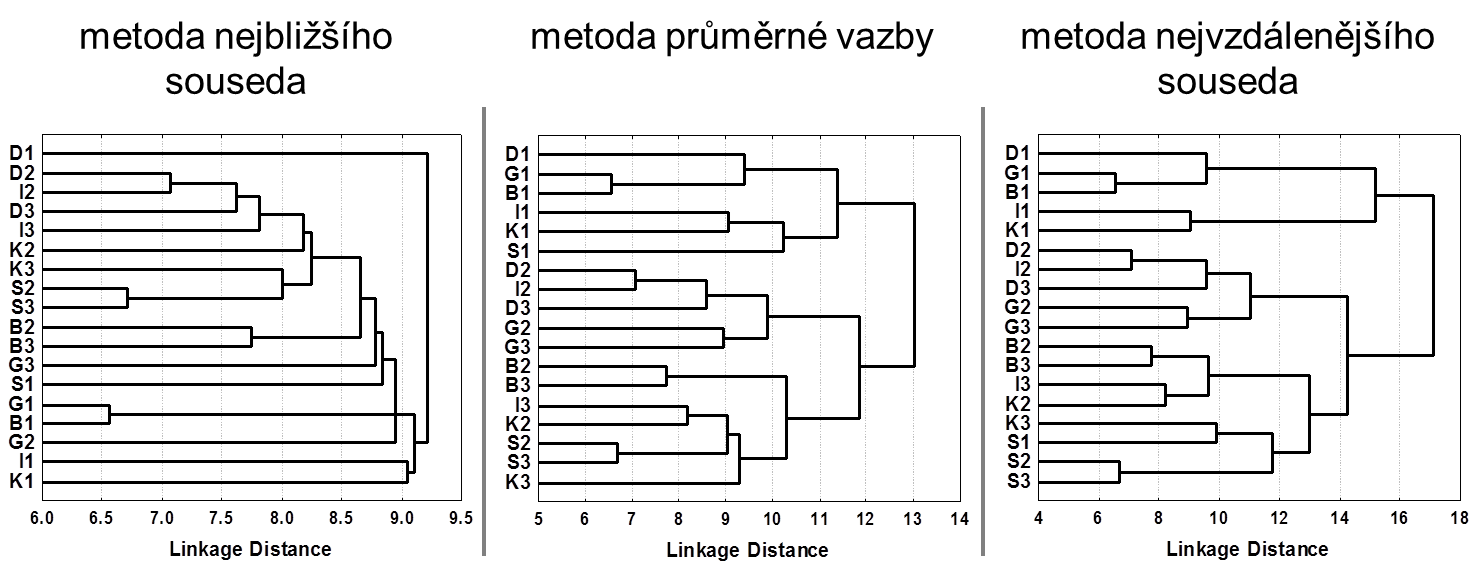Obr. 5: Dendrogramy vytvořené pomocí stejné metriky vzdálenosti (Euklidovská vzdálenost) a tří různých měr vzdálenosti mezi shluky: metody nejbližšího souseda, metody průměrné vazby a metody nejvzdálenějšího souseda. V případě metody nejbližšího souseda je zjevné silné řetězení objektů. (Společenstva korýšů šesti lokalit ve třech časových obdobích; podle [5].)

Výsledek hierarchického aglomerativního shlukování je ovlivněn na několika úrovních (Obr. 6). Jde nejenom o typ vstupních dat, ale také o jejich případnou transformaci a standardizaci, dále o měření vzdálenosti/podobnosti mezi objekty a následně o měření vzdálenosti mezi shluky. Podle Kováře a Lepše [7] mají transformace dat větší vliv na výsledek shlukování než metoda měření vzdálenosti mezi shluky.

Obr. 6: Výsledek hierarchického aglomerativního shlukování je ovlivněn na několika úrovních (podle [10]).

Může nastat situace, kdy se v asociační matici vyskytnou tzv. shody (ties) – stejné hodnoty u různých dvojic objektů, případně shluků. Dochází k tomu zejména při analýze binárních dat. Existuje několik možností řešení těchto shod v závislosti na typu vazeb mezi objekty, např. spojení všech objektů najednou, paralelní vytvoření skupin (tzv. multiple fusion), nebo náhodné spojení tzv. silent mode, při kterém je výsledek ovlyvněn pořadím objektů v primární matici; dalšími možnostmi jsou např. tzv. single linkage a suboptimal fusions. Různé způsoby vypořádání se se shodami ovšem také ovlivňují výsledný dendrogram.

Hierarchické aglomerativní metody jsou velice populární a jejich výhodou je, že výsledný dendrogram je jednoduše interpretovatelný. Tyto metody jsou vhodné ovšem pouze pro méně objemná data. Velké množství proměnných nebo objektů v dendrogramu je totiž obtížné interpretovat. Kritickým problémem hierarchické aglomerativní analýzy je, že je silně závislá na zvolení vhodné metriky vzdálenosti/koeficientu podobnosti mezi objekty a také na způsobu měření vzdálenosti mezi shluky. Jejich výběr bývá často subjektivní, musí být ovšem vhodně zvoleny vzhledem k charakteru dat a zodpovídat cíli úlohy.