Nelineární transformace dat

Většina transformací, které se používají v medicíně a biologii, jsou nelineární transformace. Tyto transformace mění rozdělení dat, lze je tedy využít pro úpravu dat, abychom se přiblížili vícerozměrné normalitě. Z nelineárních transformací se využívá:

1. Logaritmická transformace

kde x_ij je hodnota j-té proměnné u i‑tého objektu a log_c je logaritmus o základu c, přičemž se zpravidla používá dekadický logaritmus (c=10) či přirozený logaritmus (c=e, kde e je Eulerovo číslo) a v analýze dat expresí genů se často používá dvojkový logaritmus (c=2). Druhý typ transformace, kdy k proměnné přičítáme jedničku, se používá v případě, když jsou v datech přítomny nuly.

Logaritmická transformace se často používá ze čtyř různých důvodů:

• k normalizaci dat, tedy k převedení dat na normální rozdělení u proměnných s log-normálním rozdělením;
• k dosažení homogenity rozptylu;
• k linearizaci vztahu proměnných;
• k přiřazení menší váhy dominantním proměnným a zvýraznění kvalitativní stránky dat.

Při používání logaritmické transformace bychom však měli mít na paměti, že je nevhodná u dat, která jsou již v logaritmickém tvaru (např. pH).

2. Odmocninová transformace

popřípadě ve tvaru:

Tuto transformaci lze využít:

• před analýzou proměnných s Poissonovým rozdělením (např. počet jedinců určitého druhu získaných z jednoho místa za určitou časovou jednotku či počet buněk na určité ploše apod.);
• k přiřazení nižší váhy dominantním proměnným.

3. Arkussinová transformace

Arkussinová transformace je použitelná především pro proměnné s binomickým rozdělením a používá se:

• v kombinaci s odmocninovou transformací a předpokládá, že data jsou měřena v intervalu 0-1;
• na úpravu relativních hodnot vyjádřených v intervalu 0-1 (např. vegetační pokryvnosti druhů).

4. Exponenciální transformace

Pokud a je reálné číslo větší než 1, jsou zvýrazněny dominantní proměnné. Pro hodnoty  se běžně nepoužívá.

5. Transformace na ordinální škálu

Při transformaci na ordinální škálu jsou hodnoty proměnných převedeny do tříd. Čím vyšší je číslo třídy, tím vyšší byla původní hodnota. Ovšem stejné číslo třídy nemusí vždy znamenat stejnou hodnotu původní proměnné a intervaly tříd nemusí být stejné. Příkladem může být kategorizace věku na skupiny pod 20 let, 20-30 let, 30-40 let, 40-50 let, 50 a více let apod. V ekologii je typickou transformací na ordinální škálu použití Braunovy-Blanquetové stupnice při kvantifikaci pokryvnosti vegetace (Tabulka 2).

Tabulka 2. Braunova-Blanquetové stupnice pokryvnosti vegetačních druhů.

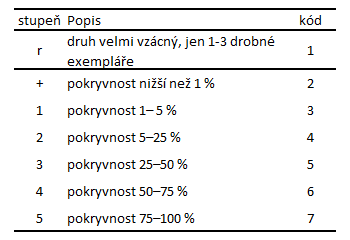
Extrémem je binarizace – transformace na prezenci a absenci.

Transformací na ordinální škálu se vždy ztrácí část informace. V některých případech je ovšem tato transformace jediná možnost, jak dosáhnout srovnatelnosti dat (např. třídy ekologického stavu).

Při sběru dat je určitě vhodné získávat co nejdetailnější data (tzn. například zjišťovat věk subjektů v letech), protože transformovat data můžeme jednoduše. Zatímco kdybychom zjišťovali u subjektů pouze, zda mají věk pod 20 let, 20-30 let atd., už nikdy nebudeme schopni zpětně zjistit skutečný věk, přestože jsme si původně mysleli, že ho potřebovat nebudeme, ale nakonec v průběhu analýz by se ukázalo, že je potřebné ho znát.