
Volba popisných proměnných
V žádném z obou přístupů ale není specifikováno, jak určit výchozí množinu proměnných. To se zpravidla děje na základě empirie a expertní analýzy vycházející ze znalosti podstaty řešeného problému. Může to být i na základě simulačních výpočtů s matematickými modely analyzovaných jevů a procesů. Neméně důležitým aspektem pro tuto počáteční volbu je i naše schopnost, daná technickými možnostmi, určité veličiny měřit. Není proto jisté, zda zvolená výchozí množina bude obsahovat právě ty veličiny, jejichž hodnoty jsou pro danou klasifikační či jinou úlohu nejužitečnější.
Přes empirický charakter počáteční volby veličin platí některé zásady, kterými se lze při této volbě řídit, především pokud provádíme volbu proměnných pro následnou klasifikaci. Podle první myšlenky, která napadne, to vypadá, že užitečnější (informativnější) pro klasifikaci by měla být ta veličina, pro kterou jsou dvě klasifikační třídy vzdálenější. Samotná vzdálenost ale sama o sobě není rozhodující. Při zvažování, zda použít tu kterou veličinu, je třeba vzít v úvahu i rozptyl hodnot uvažovaných veličin. Lze tedy formulovat dva základní principy (tyto principy se rovněž využívají u Fisherovy lineární diskriminace [Fisherova diskriminace]):
- výběr veličin s maximální vzdáleností mezi třídami
Pokud je rozptyl hodnot zvolené proměnné ve dvou klasifikačních třídách stejný, pak jsou třídy lépe rozlišitelné pro tu veličinu, pro kterou je vzdálenost mezi třídami větší (Obr.1a).
- výběr veličin s minimálním rozptylem uvnitř tříd
Když je vzdálenost dvou tříd pro různé veličiny stejná, pak jsou třídy lépe rozlišitelné s tou veličinou, jejíž hodnoty se pro každou třídu mění méně, tj. jejíž rozptyl je v jednotlivých klasifikačních třídách menší (Obr.1b). Jinými slovy, čím menší je rozptyl veličiny uvnitř klasifikační třídy, tím více informace nese veličina o třídě, do které patří.
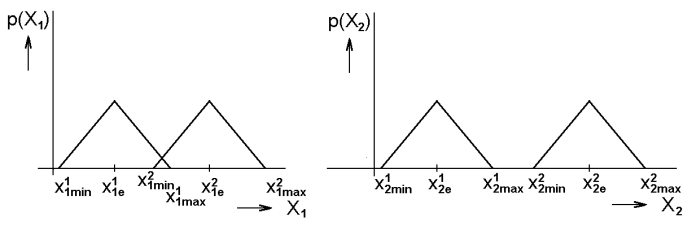 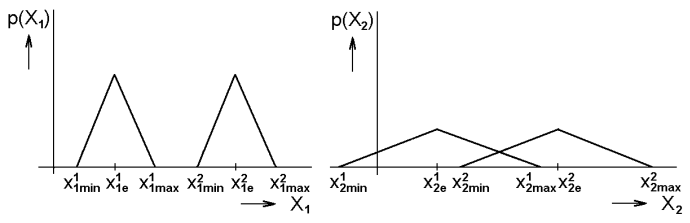 Obr.1 Zásady pro volbu proměnných – a) preference maximální vzdálenosti mezi třídami; b) preference minimálního rozptylu uvnitř tříd
|
Jestliže vyjádříme rozložení hodnot uvažovaných veličin pomocí hustoty pravděpodobnosti tak, jak je naznačeno na Obr.1, je optimální volba charakterizována minimálním překryvem obou hustot, tj. situací, která znamená minimalizaci chybných rozhodnutí Bayesův klasifikátor.
- výběr vzájemně nekorelovaných veličin
Pokud je možné hodnoty jedné proměnné odvodit z hodnot druhé proměnné, použití obou těchto proměnných potom nepřináší žádnou další informaci v analýze či klasifikaci oproti použití pouze jedné z nich, jedno které.
- výběr veličin invariantních vůči deformacím (fluktuacím, variabilitě)
Poslední požadavek je především praktický. Volba elementů formálního (matematického) popisu klasifikovaného objektu závisí na jeho charakteru, charakteru původních údajů o něm, i na způsobu předzpracování. V těch případech, kdy je odstranění deformací dat příliš náročné, případně nejde vůbec realizovat, je třeba vybrat takové veličiny, které nejsou rušením ovlivněny, resp. podstatně ovlivněny. Někdy lze výběrem veličiny fázi předzpracování eliminovat, a tak zjednodušit celé zpracování, i když jsou algoritmy předzpracování jednoduše realizovatelné.




