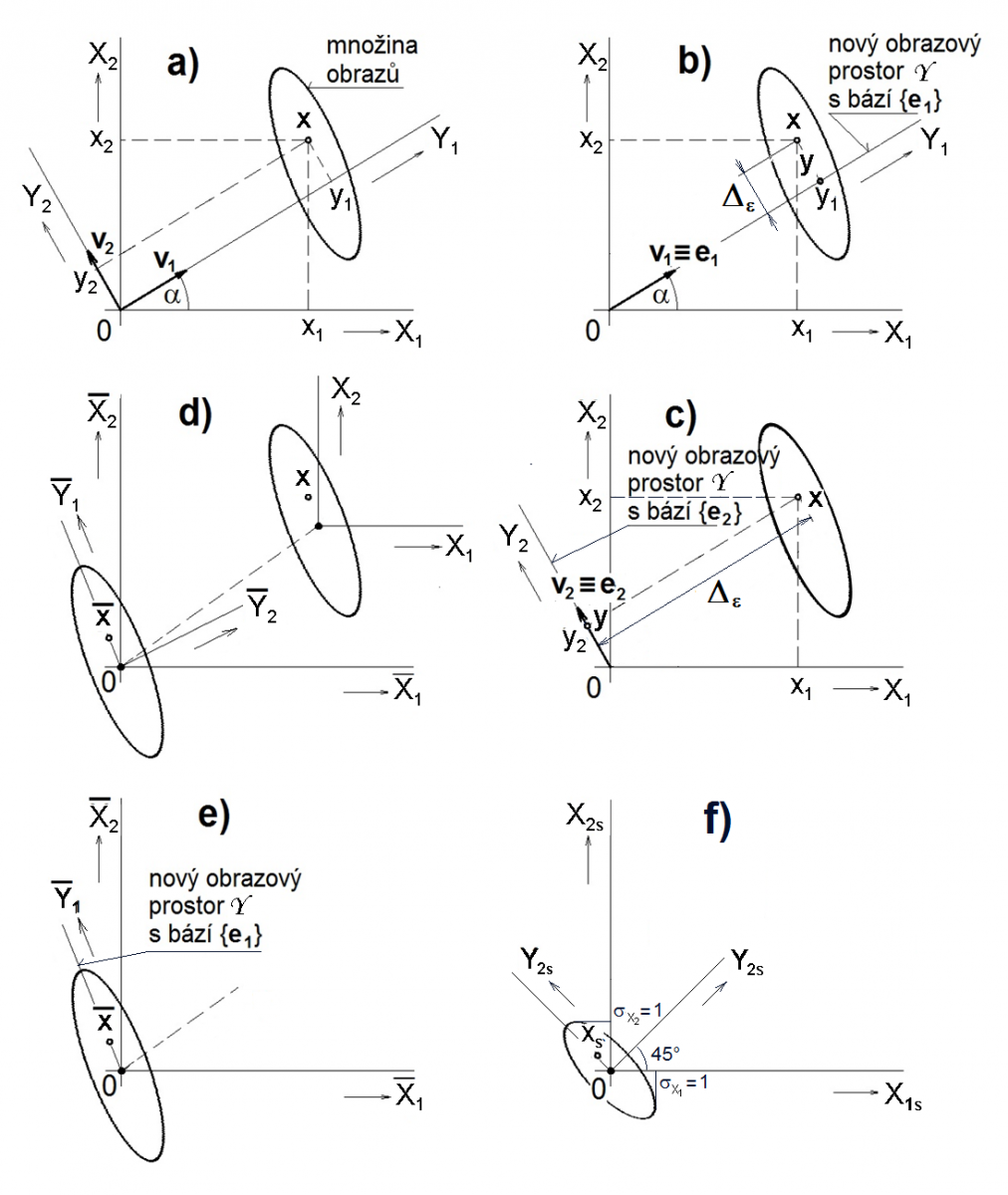
Geometrická interpretace
Diskrétní Karhunenův – Loevův rozvoj a na něj navazující analýza hlavních komponent má velice názornou matematickou interpretaci (obr.3). Nechť je původní vektorový prostor dvourozměrný a je dán veličinami a
a vektor x má tedy v původní souřadnicové soustavě souřadnice
a
. Po transformaci souřadnicového systému, která je primárně určena vlastnostmi autokorelační matice množiny vektorů, jsou souřadnice uvedeného vektoru transformovány do hodnot
a
. Vzhledem k tomu, že je transformace souřadnicové soustavy lineární, jsou obě nové souřadnice určeny lineární kombinací souřadnic původních (obr. 3a,b,c), tedy
|
|
(16)
|
Pokud nedojde k redukci rozměru vektorového prostoru, je vektor i v transformovaných souřadnicích vyjádřen zcela přesně. Omezíme-li ale počet souřadnic, vynechávají se nejdříve souřadnice, které způsobují menší střední kvadratickou chybu, jinými slovy méně přispívají k výsledné aproximaci, v zobrazeném případě je to souřadnice y2. Hodnota chyby je určena právě těmito vynechanými souřadnicemi.
Při nulovém rozptylu jsou vlastní čísla autokorelační matice rovna
a
. Vlastní vektor v1 prochází právě bodem, ve kterém leží všechny vektory, a ostatní vektory
se volí tak, aby i nový souřadnicový systém byl ortonormální. Střední kvadratická odchylka je v tom případě rovna nule.
Pokud data centrujeme (obr.3d,e), počítáme s kovarianční maticí. Pak má transformovaná bázová soustava seřazeny osy ve směrech největších rozptylů (obr.3d), které jsou v této nové souřadnicové soustavě číselně rovny vlastním číslům kovarianční matice. Vlastní čísla a vlastní vektory kovarianční matice jsou různé od vlastních čísel a vektorů autokorelační matice, proto se oba Karhunenovy – Loevovy rozvoje logicky liší.
Když originální data navíc vztáhneme ke směrodatné odchylce (standardizujeme), tj. odstraníme další možnou užitečnou informaci pro rozlišení dat, dále ztěžujeme výpočet vlastních čísel a vektorů matice korelačních koeficientů - množina vektorů získává kompaktnější, kulovitější tvar, stírá se rozdíl mezi vlivem jednotlivých nových souřadnic, z matematického hlediska autokorelační matice ztrácí dobrou podmíněnost, což v důsledku může vést i k výpočetním chybám (obr.3f).