Standardizace dat

Ke standardizaci se používají statistiky odvozené z analyzovaného souboru dat (průměr, směrodatná odchylka, rozpětí, maximum atd.). Proměnné se tímto postupem převádějí na stejné měřítko, přestává tedy záležet na skutečném rozměru příslušných proměnných. K nejčastějším úpravám patří standardizace směrodatnou odchylkou a standardizace rozpětím. Mezi další způsoby standardizace dat patří standardizace na celkový součet řádku či sloupce, standardizace na maximum řádku či sloupce a standardizace na jednotkovou délku vektoru řádku, které se používají zejména ve shlukové analýze v ekologických studiích.

1. Standardizace směrodatnou odchylkou

Jedná se o nejčastější způsob standardizace. V literatuře se dokonce pod pojmem „standardizace“ často uvádí pouze tento typ úpravy hodnot j-té proměnné (tedy j-tého sloupce matice X), kdy se nová hodnota získá odečtením výběrového průměru  této proměnné od původní hodnoty a podělením směrodatnou odchylkou  této proměnné ( je současně j-tý diagonální prvek výběrové kovarianční matice S):

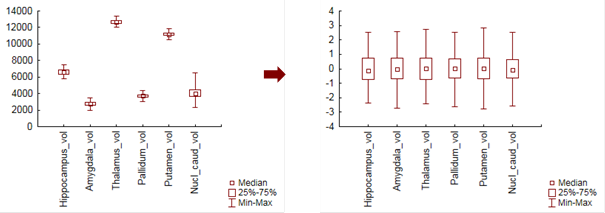
Výsledná standardizovaná proměnná má tedy nulový průměr a rozptyl roven jedné. Rozsah nové proměnné bude přibližně od -3 do 3, pokud měla původní proměnná normální rozdělení. Ukázka krabicových grafů původních a standardizovaných proměnných je na Obr. 6. Výsledná hodnota  je současně tzv. z-skóre, které vyjadřuje, o kolik směrodatných odchylek se i-tá hodnota odchýlila od průměru.

Přestože je standardizace dat široce používána, neměli bychom ji provádět automaticky a bez důkladného promyšlení, protože může vést ke ztrátě informace (např. může vést k horším výsledkům klasifikace). Navíc standardizace není vhodná v případě, když proměnné nemají normální rozdělení a když se v datech vyskytují odlehlé hodnoty.

2. Standardizace rozpětím

Standardizace rozpětím neboli „min-max normalizace“ se doporučuje se použít v případech, kdy mají proměnné různý rozsah, ale nemají normální rozdělení či obsahují odlehlé hodnoty. Standardizace rozpětím se provede následujícím způsobem:

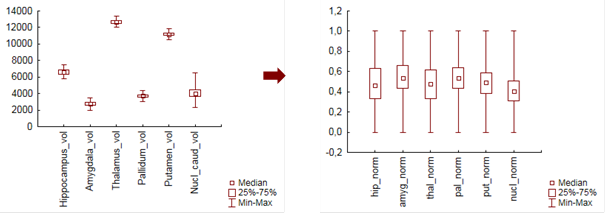
Rozsah hodnot proměnných po min-max normalizaci je od 0 do 1 (Obr. 7).

3. Standardizace na celkový součet řádku

U tohoto typu standardizace se hodnoty proměnných pro daný objekt sečtou a každá hodnota je vydělená tímto součtem:

V ekologických studiích se takto určí relativní abundance (dominance) druhů. V případě, že jsou součty řádků velmi rozdílné, je třeba používat tuto standardizaci opatrně, protože vzácné druhy se objevují až ve vzorcích s vysokým počtem jedinců.

4. Standardizace na celkový součet sloupce

Tento typ standardizace je obdobou předchozího typu standardizace, pracuje se však se součtem hodnot ve sloupci. Tedy pro každý sloupec (proměnnou) je určen součet přes všechny objekty. Původní hodnoty jsou pak poděleny příslušným sloupcovým součtem:

V ekologických studiích, kde proměnné představují jednotlivé druhy, tímto způsobem získáme frekvence druhů v objektech. Tato standardizace silně nadváží vzácné druhy a podváží běžné druhy, protože všechny početnosti jsou vyjádřeny jako procento ze sumy druhů napříč lokalitami. Proto se tato standardizace doporučuje pouze tehdy, když se frekvence druhů výrazně neliší. Tato standardizace bývá používána v případech, kdy se v seznamu druhů vyskytují různé trofické úrovně, protože vyšší trofické úrovně jsou méně zastoupeny (a proto může vyhovovat jejich nadvážení).

5. Standardizace na maximum řádku

Principem tohoto typu standardizace je, že jsou všechny hodnoty v řádku (tedy všechny hodnoty proměnných pro daný objekt) poděleny maximální hodnotou dosaženou u některé proměnné v řádku:

Tato standardizace bývá aplikovaná ze stejného důvodu jako standardizace na celkový součet řádku. Je méně citlivá na počet proměnných, je ovšem potřeba užívat ji opatrně v těch případech, kdy jsou veliké rozdíly ve vyrovnanosti vzorků.

6. Standardizace na maximum sloupce

Obdobně jako u předchozího typu standardizace, jsou všechny hodnoty v sloupci poděleny maximální hodnotou sloupce (tedy maximální hodnotou dané proměnné):

Tato standardizace je v ekologických studiích doporučovaná, podobně jako standardizace na celkový součet sloupce, když jsou přítomny různé trofické úrovně.

7. Standardizace na jednotkovou délku vektoru řádku

U tohoto typu standardizace se podělením hodnot proměnných u objektu odmocninou sumy čtverců hodnot všechny vektory objektů zobrazí na jednotkové sféře prostoru tvořeného proměnnými (v ekologických studiích jde o druhy).