Ověření normality vícerozměrných dat

Pro ověření normality jednorozměrných dat je možné použít grafické metody i statistické testy. Z grafických metod se používá vykreslení histogramu či Q-Q diagramu a ke statistickému testování můžeme zvolit Shapirův-Wilkův test či Kolmogorovův-Smirnovovův test .

U ověřování víceroměrné normality dat nám bohužel nestačí ověřit normalitu každé proměnné zvlášť, protože i když mají jednotlivé proměnné normální rozdělení, dohromady mít vícerozměrné normální rozdělení nemusejí (viz Obr. 2, ze kterého je patrné, že se v datech vyskytuje vícerozměrná odlehlá hodnota). K ověření vícerozměrné normality můžeme také použít grafické metody a statistické testy.

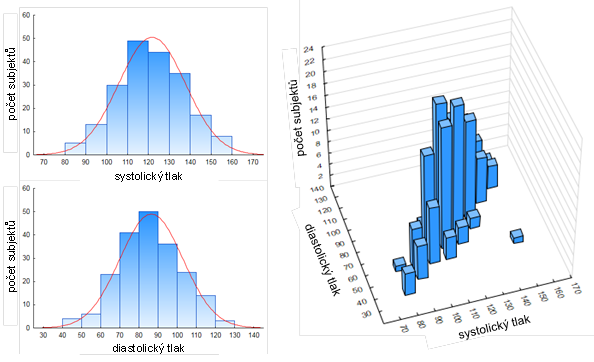
Začněme nejprve ověřením dvourozměrné normality. Hodnoty dvou proměnných můžeme vykreslit pomocí bodového grafu. Pokud mají proměnné dvourozměrné normální rozdělení, budou body tvořit obrazec elipsy. Z podkapitoly o vícerozměrném rozdělení [odkaz na podkapitolu 2.3.1 tohoto souboru] již víme, že Mahalanobisova vzdálenost hodnot proměnných od vektoru výběrových průměru d² má chí-kvadrát rozdělení s p stupni volnosti, můžeme tedy očekávat, že pokud je splněn předpoklad dvourozměrné normality, 100q% hodnot bude ležet uvnitř elipsy dané nerovnicí:

,

(17)

kde v_q(2) je 100q% kvantil chí-kvadrát rozdělení se dvěma stupni volnosti. Tento poznatek můžeme rozšířit pro ověření troj- a vícerozměrné normality, budeme pak pouze čekat, že 100q% hodnot bude ležet uvnitř elipsoidu namísto elipsy. Ilustrace ověření dvourozměrné normality pomocí elipsy konstantní hustoty pravděpodobnosti je na Obr. 3.

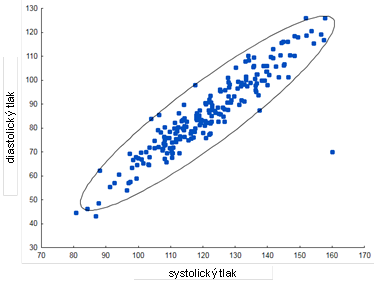
Obr. 3: Ukázka ověření normality pomocí elipsy konstantní hustoty při zvolení kvantilu q=0,95. Body tvoří obrazec elipsy a 95% bodů leží uvnitř elipsy, což by ukazovalo na dvourozměrnou normalitu systolického a diastolického tlaku, v datech se však vyskytuje odlehlá hodnota.

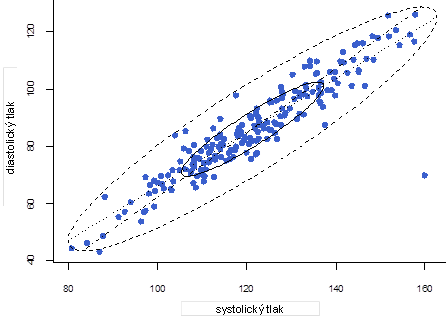
Další grafickou metodou použitelnou pro ověření dvourozměrné normality je tzv. „bagplot“, který je označován jako „dvourozměrný krabicový graf“ (bivariate boxplot). Ukázka tohoto grafu je na Obr. 4. Bagplot sestává ze dvou koncentrických elips, z nichž vnitřní obsahuje 50% dat a vnější vymezuje oblast bez odlehlých hodnot, což je analogické klasickému krabicovému grafu. Tento typ grafu je tedy velmi vhodný pro detekci vícerozměrných odlehlých hodnot. Navíc jsou v tomto grafu znázorněny i regresní přímky závislosti první proměnné na druhé a druhé proměnné na první. Úhel mezi regresními přímkami je malý pro vysoké hodnoty korelací (v absolutní hodnotě), zatímco pro nízké hodnoty korelací (blízké nule) je úhel velký.

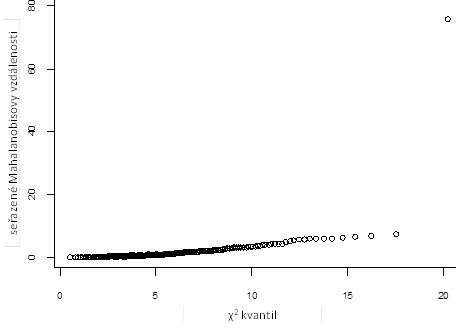
Ani jedna z uvedených grafických metod však bohužel neumožní vizualizaci čtyř- a vícerozměrných dat. Lze si ovšem pomoci tím, že si vektor hodnot p proměnných popisujících daný objekt převedeme na jedno číslo, konkrétně na již dobře známou Mahalanobisovu vzdálenost (8) . Poté můžeme vykreslit objekty seřazené podle Mahalanobisovy vzdálenosti proti odpovídajícím kvantilům chí-kvadrát rozdělení s p stupni volnosti. Pokud data splňují předpoklad vícerozměrného normálního rozdělení, budou body ležet na přímce vedoucí od levého dolního do pravého horního rohu grafu (obdobně jako u Q-Q diagramu). Tento typ grafu se někdy označuje jako „diagram χ²“ a jeho ukázka je uvedena na Obr. 5.

Ze statistických testů lze pro ověření vícerozměrné normality použít například testy založené na vícerozměrné šikmosti a špičatosti. Problémem statistických testů pro ověření jednorozměrné i vícerozměrné normality však je, že velmi snadno zamítnou hypotézu, že data mají vícerozměrné normální rozdělení, pokud je velký rozsah souboru. A naopak, pokud je soubor malý, statistické testy často řeknou, že data mají normální rozdělení, přestože se v datech vyskytují odlehlé hodnoty. Je to vcelku paradoxní situace, protože u velkých datových souborů nám drobné odchylky od normality nevadí a vliv odlehlých hodnot na výsledky analýzy jsou minimální. Zatímco u malých souborů mohou odlehlé hodnoty výsledky ovlivnit znatelně. Statistické testy je tedy vhodnější používat spíše orientačně. Z tohoto důvodu nejsou statistické testy na ověřování normality v těchto učebních materiálech rozebírány podrobněji. Zájemcům o detailnější popis těchto testů lze doporučit monografii [3].

Pokud pomocí grafických metod (nebo případně statistických testů) zjistíme, že data nesplňují předpoklad vícerozměrného normálního rozdělení, máme dvě možnosti, jak dále postupovat:

1. využít neparametrické metody (neparametrické vícerozměrné metody však často nebývají implementované ve statistických softwarech a nejsou s nimi zatím zpravidla velké zkušenosti, proto použití těchto metod a interpretace jejich výsledků může být obtížná);
2. transformovat data tak, aby byl předpoklad normality splněn nebo abychom se vícerozměrné normalitě alespoň co nejvíce přiblížili.

Transformacím dat je věnována následující podkapitola.