Prokrustova analýza

Jiný možný přístup pro porovnávání dvou vícerozměrných prostorů představuje Prokrustova analýza. Jedná se především o ordinační metodu, která srovnává dva ordinační prostory. Jejím účelem je najít kompromis mezi ordinacemi pro dvě datové matice obsahující stejné objekty použitím „algoritmu rotace – dolehnutí“ (rotation – fit algorithm), který minimalizuje sumu čtverců vzdáleností mezi odpovídajícími si body ze dvou asociačních matic ve vícerozměrném euklidovském prostoru. Výsledkem ordinace je, že má každý objekt dvě reprezentace, z každé matice jednu. Tak můžeme vykreslit v xy grafu rozdíl mezi těmito dvěma originálními maticemi.
Prokrustova analýza vyžaduje, aby měly vstupní datové matice stejný rozměr. Když tato podmínka není splněna, je matice s menším počtem sloupců doplněna o nulové vektory, dokud není dosaženo stejného počtu sloupců.
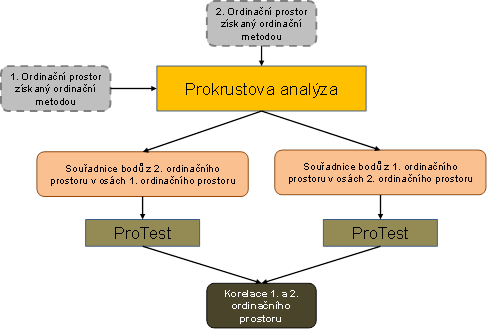
Zjednodušené schéma Prokrustovy analýzy a metod na ní navazujících je zobrazeno na Obr 3. Postup výpočtu Prokrustovy analýzy je následující:
Nejdříve je nutné provést centrování a škálování, kdy jsou dvě vstupní datové matice (rozměru ) a (rozměru ) standardizovány tak, aby měly před rotací celkový rozptyl roven 1. Toto získáme pomocí Gowerovy standardizace, která sestává z podílů každé hodnoty ve sloupcově centrované matici a čtverce celkového rozptylu matice, který je zároveň čtverec sumy vlastních čísel dané matice.
Následně se spočítá kovariance dvou matic standardizovaných dle Gowera ( a ) pomocí vzorce

(5)

V dalším kroku jsou získány singulární hodnoty kovarianční matice  (rozměru ) pomocí rozkladu na singulární hodnoty:

(6)

kde  je matice rozměru , je matice rozměru a je diagonální matice rozměru , jejíž diagonální prvky jsou singulární hodnoty.
Dále spočítáme stopu matice jako sumu všech diagonálních prvků matice (tedy jako sumu singulárních hodnot):

(7)

Protože jsou singulární hodnoty pozitivní nebo rovné nule, je tato suma vždy nezáporná.
Poté získáme statistiku , která udává hodnotu sumy čtverců vzdáleností:

(8)

Statistika  nabývá hodnoty mezi nulou a jedničkou. Kdyby měly matice a jen jednu proměnnou, by byla rovna Pearsonovu korelačnímu koeficientu a pak . Statistika  je dále testovaná permutačním procesem, stejně jako Mantelův test. Tato procedura bývá nazývaná Prokrustův randomizační test (Procrustean randomization test – ProTest).
V dalším kroku Prokrustovy analýzy spočítáme optimální rotační matici, kterou získáme jako

(9)

kde Tr(W) hraje roli škálovacího vektoru. Následně je matice  vykreslena pomocí optimální rotace  nad matici . Objekty v grafu jsou tedy kresleny pomocí matice  a .