Výpočetní algoritmus

Cílem NMDS je najít konfiguraci bodů (souřadnic, vzdáleností, disparit) minimalizující ztrátovou funkci. Minimalizace ztrátové funkce probíhá pomocí iterativního algoritmu ve dvou krocích:

1. Hledání optimální monotónní transformace dat (optimální škálování);
2. Hledání optimálních souřadnic (odhad parametrů).

Celý iterativní algoritmus je pak obecně popisován ve čtyřech krocích (Obr. 5):

1. Určení rozměrů a výchozí matice souřadnic (počáteční konfigurace);
2. Optimální škálování - nemetrická fáze (výpočet disparit );
3. Odhad parametrů - metrická fáze (výpočet souřadnic);
4. Determinace hodnoty ztrátové funkce (STRESS).

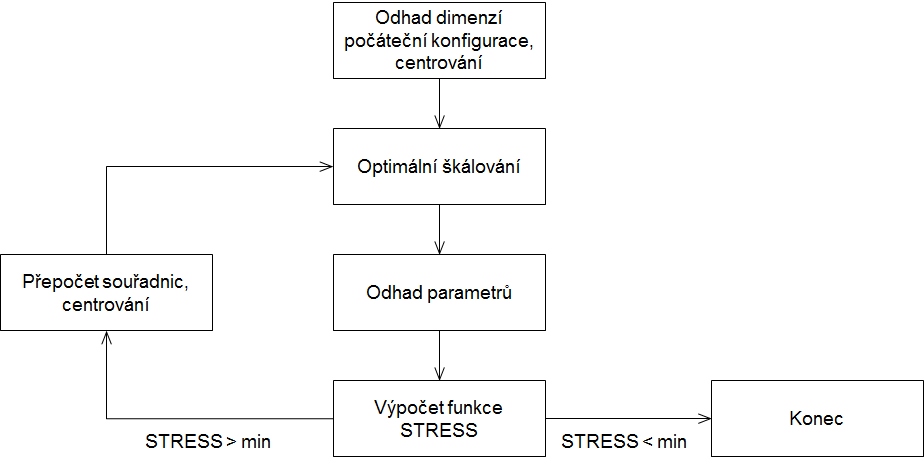Obr. 5: Algoritmus nemetrického vícerozměrného škálování.

Výchozím krokem je určení počáteční konfigurace pro objektů v -rozměrném prostoru. Prvním krokem výpočtu je tedy uspořádání všech souřadnic objektů v množině do vektoru s prvky . Tento vektor použijme jako souřadnice objektů v počáteční konfiguraci, kterou označíme . K jejímu určení můžeme použít několik různých metod, může být odvozena z výsledků analýzy hlavních komponent nebo analýzy hlavních koordinát, nebo např. i jednoduchým generováním náhodných čísel. Konfiguraci je vhodné centrovat do středu souřadného systému.

Ze souřadnic počáteční konfigurace (případně konfigurace z poslední iterace) provedeme odhad disparit  a hodnoty ztrátové funkce STRESS. Během této fáze zůstávají hodnoty souřadnic i vzdáleností konstantní. Je-li hodnota STRESSu menší než předem zvolené nízké číslo (obvykle 0,001), výpočet končí. Není-li podmínka splněna, probíhá další přepočet spočívající v odhadu nových souřadnic, disparit a hodnoty ztrátové funkce. Výpočet nových souřadnic vychází z odhadů nových disparit a odhadů souřadnic a vzdáleností v minulé iteraci. Kritériem kvality konfigurace je funkce STRESS. V této fázi zůstávají konstantní hodnoty disparit . Iterativním procesem je nalezeno lokální minimum ztrátové funkce (minimální hodnota STRESS-u pro dané nastavení počtu rozměrů). Celý proces končí buď dosažením požadované velikosti funkce STRESS, nebo po dosažení určitého počtu iterací.

Výsledkem výpočtu jsou pak souřadnice všech objektů v -rozměrném prostoru; tj. výsledná konfigurace bodů znázorňující v grafickém zobrazení vzájemné vztahy objektů. Uspořádání je závislé na počtu zvolených dimenzí ().

Při NMDS je jedním z klíčových kroků rozhodnutí o počtu použitých rozměrů. Pro různá nastavení počtu rozměrů spočítáme výsledné hodnoty STRESSu. Se zvyšujícím se počtem rozměrů hodnota STRESSu klesá, hodnoty lze vykreslit do grafu. Zobrazení závislosti STRESSu na počtu rozměrů bývá užitečné k rozhodnutí o skutečném počtu rozměrů, které budou použity. Obecně platí, že čím víc dimenzí používáme k reprodukci matice vzdáleností, tím lépe výsledná konfigurace vysvětluje pozorované vzdálenosti v původních datech (tj. tím menší je STRESS). Samozřejmě naším cílem je redukce pozorovaných dat, tj. vysvětlit matici vzdáleností pomocí menšího počtu dimenzí. Získané rozměry by ale měly být interpretovatelné. Každému rozměru by měl být přiřazen věcný význam. V NMDS je pořadí os náhodné: první osa není nutně důležitější než druhá osa, atd. Proto je někdy užitečné výslednou konfiguraci v souřadném systému rotovat a tím usnadnit interpretaci výsledku.

Kvalitu celého modelu můžeme hodnotit podle výsledné hodnoty STRESSu (Tab. 11).

Tabulka 11: Kvalita modelu NMDS

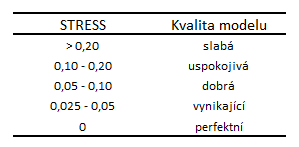
Tato tabulka nám může být nápomocná i při určení správného počtu rozměrů. Obecně není nutné redukovat počet rozměrů do té míry, že STRESS přesáhne hodnotu 0,1. Podobně není potřeba zvyšovat počet rozměrů když STRESS je již menší než 0,05.