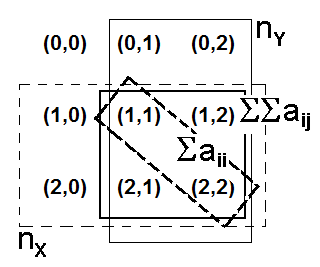Metriky pro určení podobnosti dvou obrazů s kvantitativními hodnotami souřadnic

Metriky podobnosti pro vektory s kvalitativními hodnotami souřadnic, resp. vektorů s diskrétními hodnotami je vhodné rozdělit na případy obecné a případy s dichotomickými hodnotami, pro které je definována celá řady tzv. asociačních koeficientů. Asociační koeficienty až na výjimky nabývají hodnot z intervalu , hodnoty 1 v případě shody vektorů, 0 pro případ nepodobnosti.

První možností, jak definovat metriku podobnosti pro nedichotomické hodnoty, je odvodit ji z Hammingovy metriky

kde b_max je maximální hodnota, které může Hammingova vzdálenost nabývat, tj. hodnota rozměru srovnávaných vektorů.

Zřejmě nejrozšířenější metrikou podobnosti dvou vektorů je ale tzv. Tanimotova metrika podobnosti (název opět není jen náhodnou podobností s názvem metriky uvedené v kap. Metriky pro určení podobnosti mezi dvěma obrazy s kvalitativní-mi hodnotami souřadnic tohoto textu, vztah 30 ). Často se používá například v chemii při porovnávání vzorců chemických sloučenin. Její princip vychází z postupu srovnání dvou množin.

Jinými slovy, Tanimotova podobnost dvou množin je určena počtem společných prvků obou množin vztaženým k počtu všech rozdílných prvků.

Využijme nyní tohoto principu pro stanovení podobnosti dvou obrazových vektorů s kvalitativními, resp. diskrétními hodnotami proměnných. Pro výpočet Tanimotovy podobnosti jsou pak použity všechny páry složek srovnávaných vektorů, kromě těch, jejichž hodnoty jsou obě nulové.

Tuto volbu se pokusme zdůvodnit případem, kdy analyzujeme vektory ordinálních kvalitativních proměnných, přičemž hodnotu i-té složky daného vektoru považujeme za míru výskytu určitého jevu popisovaného právě i-tou proměnou. Podle této interpretace jsou páry složek vektorů s oběma hodnotami nulovými méně důležité než ostatní. Tento problém úzce souvisí i s tzv. problémem „dvojité nuly“, který se vyskytuje např. při analýze environmentálních dat (to, že se např. sledovaný druh na dvou sledovaných lokalitách nevyskytuje, není pro posouzení kvality obou lokalit tak důležité, jako společný výskyt jiných druhů). Při řešení některých úloh může být stanovení absence nějakého sledovaného rysu i principiálně nemožné – detekce určitých tvarových prvků v časové řadě.

 Hodnoty Tanimotovy podobnosti se vyskytují v intervalu od 0 při nepodobnosti do 1 při úplné shodě obou vektorů.

Příklad 6.1

Určete hodnoty Tanimotových podobností s_TQ(x,x), s_TQ(x,y) a s_TQ(x,z), jsou-li vektory x = (0, 1, 2, 1, 2, 1)^T a y = (1, 0, 2, 1, 0, 1)^T a z = (2, 0, 0, 0, 0, 2)^T.

Řešení:

Ze zadání vyplývá, že množina symbolů F = {0, 1, 2}, k = 3, n = 6.

Kontingenční tabulky jsou

;;

V prvním případě při maximální podobnosti jsou nenulové prvky kontingenční tabulky pouze na hlavní diagonále, v případě nejmenší podobnosti jsou naopak na hlavní diagonále jen nulové prvky.

V případě první podobnosti s_TQ(x,x) je n_x = 5, n_y = 5, součet prvků na hlavní diagonále a_ii také 5 a konečně součet a_ij opět 5. Hodnota podobnosti pak po dosazení je

 Pro podobnost s_TQ(x,y) je n_x = 5, n_y = 4, součet prvků na hlavní diagonále a_ii = 3 a konečně součet a_ij = 3. Hodnota podobnosti pak po dosazení je

Konečně, pro podobnost s_TQ(x,z), což představuje srovnání dvou nejméně podobných vektorů, je n_x = 5, n_y = 2, součet prvků na hlavní diagonále a_ii = 0 a konečně součet a_ij = 1. Hodnota podobnosti pak po dosazení je

Další míry podobnosti vektorů x,y  F ⁿ jsou definovány pomocí různých prvků kontingenční matice A(x,y). Některé z nich používají pouze počet shodných pozic v obou vektorech (ovšem s nenulovými hodnotami; tzv. asymetrické míry podobnosti), jiné míry používají i shodu s nulovými hodnotami (tzv. symetrické míry podobnosti). Příkladem metriky podobnosti z první uvedené kategorie může být např. metrika definovaná vztahem

nebo i metrika

Příkladem metriky druhé uvedené skupiny je např.

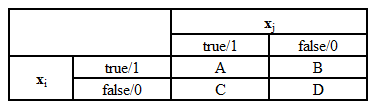
 Při řešení dichotomických problémů, tj. když k = 2, nabývá kontingenční tabulka tvar podle Obr.3, který vyjadřuje čtyři možné situace:

1. hodnota k-té souřadnice obou vektorů signalizuje, že u obou vektorů sledovaný jev nastal (obě odpovídající si proměnné mají hodnotu true) – pozitivní shoda;
2. ve vektoru x_i jev nastal (x_ik = true), zatímco ve vektoru x_j nikoliv (x_jk = false);
3. u vektoru x_i jev nenastal (k-tá souřadnice má hodnotu x_ik = false), zatímco u vektoru x_j ano (x_jk = true);
4.  sledovaný jev nenastal (obě odpovídající si proměnné mají hodnotu false) – negativní shoda.

Při výpočtu podobnosti dvou vektorů sledujeme kolikrát pro všechny souřadnice obou vektorů x_j a x_j nastaly případy shody či neshody – A+D určuje celkový počet shod, B+C celkový počet neshod a A+B+C+D = n, tj. celkový počet souřadnic obou vektorů.

Pokud budeme pokračovat v popisu Tanimotovy metriky podobnosti, pak pro dichotomické proměnné se výpočet, s ohledem na symboliku podle Obr.3, transformuje do vztahu (často je též označován jako Jaccardův-Tanimotův asociační koeficient)

což je díky zjednodušení i dichotomická varianta metriky podle vztahu (46). Tento vztah se dominantně používá v ekologických studiích.

Dichotomická varianta vztahu (47) je tzv. Russelův - Raoův asociační koeficient.

Vztah (49) modifikovaný pro dichotomické aplikace

se označuje jako Sokalův - Michenerův asociační koeficient.

Kromě uvedených koeficientů se v odborné literatuře vyskytují i Dicův (Czekanowského) koeficient (nazývaný rovněž jako Sørensenův koeficient)

a Rogersův - Tanimotův koeficient

které zvyšují význam shod v datech – v případě Dicova koeficientu zvýšením váhy počtu pozitivních shod v čitateli i jmenovateli, v druhém případě zvýšením váhy počtu neshod ve jmenovateli.

Hamanův koeficient

nabývá na rozdíl od všech dříve uvedených koeficientů hodnot z intervalu . Hodnoty -1 nabývá, pokud se hodnoty pouze neshodují; je roven nule, když je počet shod a neshod v rovnováze; a nabývá hodnoty +1 v případě úplné shody všech hodnot.

V případě Jaccardova a Dicova koeficientu je třeba vyřešit jejich hodnotu, když A = B = C = 0 (pokud jsou používány v situacích, kdy může nastat úplná negativní shoda). Pak zpravidla předpokládáme, že S_JT(x,y) = S_DC(x,y) = 1

Z asociačních koeficientů, které vyjadřují míru podobnosti, lze jednoduše odvodit i míry nepodobnosti (vzdálenosti) pomocí formule

Na základě četností A až D lze pro případ binárních hodnot vytvářet i zajímavé vztahy pro již dříve uvedené míry:

Hammingova metrika

Euklidova metrika

Pearsonův korelační koeficient

i jiné.

Příklad 6.2

Ukažte, že pro binární hodnoty souřadnic obou vektorů platí pro Euklidovu metriku vztah (58).

Skryté řešení:

Euklidova metrika je obecně definována podle vztahu (17) jako

.

Protože jednotlivé složky obou vektorů nabývají pouze binárních hodnot, pak mohou nastat pouze následující situace

• hodnoty se shodují (obě souřadnice nabývají hodnoty 0 nebo 1 a jejich rozdíl je proto nulový), což odpovídá četnostem A a D ve čtyřpolní tabulce a jejich součet A + D je proto také nulový;
• se neshodují a jejich rozdíl i jeho kvadrát je jednotkový. Počet neshod je tedy daný součtem B + C, což odpovídá součtu všech kvadrátů rozdílů souřadnic srovnávaných vektorů.

Konečně, jelikož je Euklidova metrika definována pomocí odmocniny ze součtu kvadrátů rozdílů souřadnic, součet B+C  odmocníme.