Souvislost klasifikace podle minimální vzdálenosti s dalšími principy klasifikace

Začněme se srovnáním klasifikace podle minimální vzdálenosti a klasifikací podle diskriminačních funkcí. Uvažme příklad dvou tříd reprezentovaných etalony  a  v dvourozměrném euklidovském prostoru. Výpočet vzdálenosti mezi subjektem  a libovolným z obou etalonů je v tomto prostoru definován vztahem

(3)

Podle definice rozhodovacího pravidla klasifikátoru podle minimální vzdálenosti hledáme menší z obou vzdáleností, tj. . Protože nám nejde o stanovení konkrétní vzdálenosti, ale o nalezení minima a rovněž díky tomu, že vzdálenost mezi dvěma body prostoru je vždy kladná, můžeme psát, že hledáme . To znamená, že

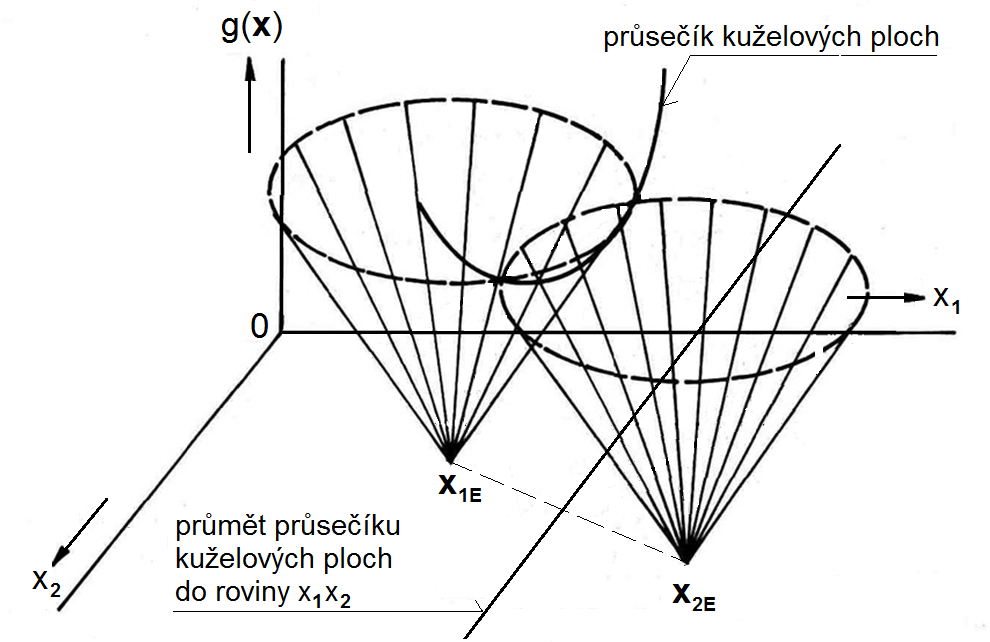
Výraz ve složených závorkách představuje pro každý etalon kuželovou plochu s vrcholem v daném etalonu (pokud je vektor totožný s etalonem, je výraz ve složených závorkách roven nule) a rozšiřující se do kladných hodnot funkce , přičemž pro souřadnice vektoru  je hodnota výrazu ve složených závorkách rovna  (Obr. 5). Jak je z obrázku patrné, tato orientace kuželové plochy bohužel nesplňuje podmínku pro diskriminační funkci. Ovšem dvojčlen  ve složených závorkách ve výrazu (4) nezávisí na klasifikační třídě pro daný vektor , proto jej můžeme považovat za aditivní konstantu, která se nepodílí na rozhodování. Poněvadž je tento člen vždy kladný, můžeme určit minimum celého výrazu právě tehdy, když najdeme ve vztahu (4) maximum výrazu v hranatých závorkách. Tím se orientace kuželové plochy mění a v souladu s principem klasifikace podle diskriminačních funkcí lze tento výraz považovat za definiční vztah diskriminační funkce -té třídy . Kuželové plochy se v obou případech protínají v parabole a její průmět do obrazové roviny je přímka (viz. Obr. 5), která je definovaná vztahem

(5)

Tato hraniční přímka mezi klasifikačními třídami je vždy kolmá na spojnici obou etalonů a tuto spojnici půlí. Z uvedeného plyne, že klasifikátor pracující na základě minimální vzdálenosti je ekvivalentní lineárnímu klasifikátoru s diskriminačními funkcemi. Dále je tento příklad ukázkou toho, že i nelineární diskriminační funkce může vyústit v lineární separaci klasifikačních tříd.

Jinou možností, jak zkonstruovat diskriminační funkci na základě principu stanovení vzdálenosti, resp. podobnosti mezi klasifikovaným obrazem a etalony klasifikačních tříd, je použití metriky podobnosti. Dle závislosti mezi vzdálenostní a podobnostní metrikou se mění tvar kuželové plochy, nicméně její vrchol leží vždy nad etalony klasifikačních tříd a kuželová plocha se rozšiřuje směrem k obrazovému prostoru. Mění se sice tvar průsečíků kuželových ploch odpovídajících jednotlivým etalonům, ale jejich průmět do obrazové roviny zůstává lineární – za předpokladu, že metriky pro jednotlivé etalony nejsou různě váhované.

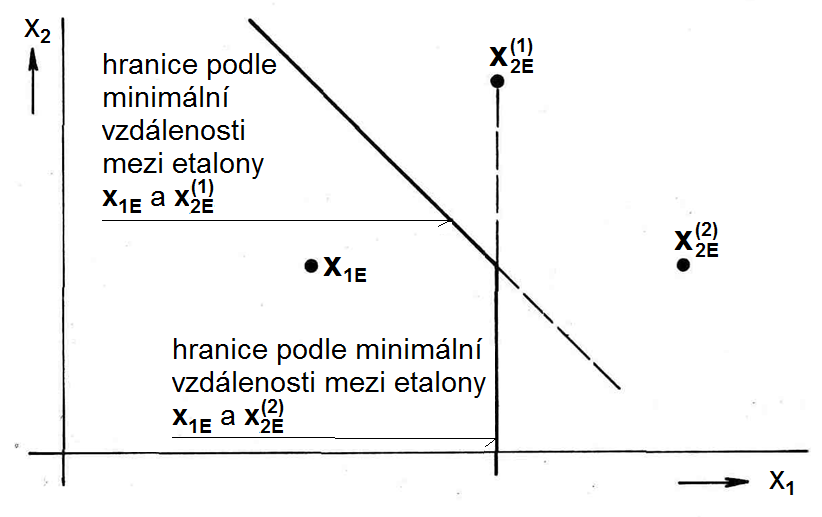
Mějme nyní případ, kdy je třída reprezentována etalonem a třída dvěma etalony  a , přičemž subjekt klasifikujeme opět pomocí kritéria nejmenší vzdálenosti. Protože třídu představují dva etalony, je hranice mezi oběma třídami lomená přímka půlící vzdálenosti mezi etalony a  a etalony a  (Obr. 6). Klasifikace podle minimální vzdálenosti s třídami reprezentovanými více etalony je tedy ekvivalentní klasifikaci s po částech lineární hranicí.