Úvod do analýzy nezávislých komponent

Analýza nezávislých komponent (ICA – Independent Component Analysis) je podobně jako analýza hlavních komponent postup, který umožňuje v původních datech odhalit skryté veličiny, které nelze přímo měřit, ovšem mohou být určitým způsobem věcně interpretovány. Zatímco analýza hlavních komponent hledá pomocí lineární transformace nové proměnné, které nejlépe reprezentují data z hlediska střední kvadratické chyby, metoda analýzy nezávislých komponent používá k lineární separaci jednotlivých složek kritérium statistické nezávislosti. Na rozdíl od analýzy hlavních komponent není primárním cílem analýzy nezávislých komponent redukce počtu popisných proměnných, ve svém důsledku, tj. po odhalení nezávislých skrytých zdrojů dat, však i ICA může vést ke snížení rozměru dat. Dalším rozdílem obou metod je rovněž skutečnost, že zatímco metoda hlavních komponent může najít uplatnění při zpracování statických i dynamických, doménou analýzy nezávislých komponent je více zpracování dynamických dat, tj. časových řad. Nicméně, není to jediné možné využití.

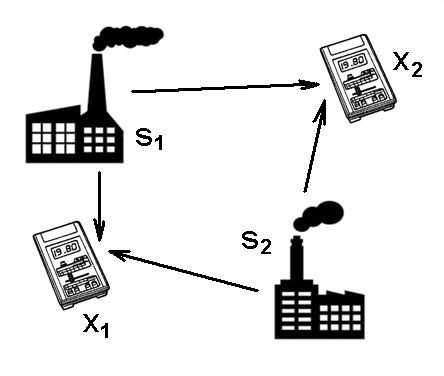
Nyní si vysvětlíme princip analýzy nezávislých komponent pomocí příkladu. Předpokládejme, že v daném prostoru jsou dva nezávislé zdroje znečištění (Obr. 1). Označme veličiny, které je charakterizují, jako a . Dále předpokládejme, že celková úroveň znečištění je měřena přinejmenším stejným počtem měřicích přístrojů, jejichž výstupy označme a . V případě, že zanedbáme možné prostorové vlivy (např. dobu šíření znečištění od zdroje k měřícímu zařízení) a nelinearity, můžeme si naměřené veličiny vyjádřit pomocí vztahů

(1)

kde parametry popisují přenosové vlastnosti prostředí, jímž se znečištění šíří, směrové charakteristiky, apod. Proměnné nazýváme skryté, nebo latentní proměnné a hodnoty x_i reprezentují pozorované veličiny, které tvoří vektor pozorování. Cílem analýzy je ze známých hodnot a určit hodnoty proměnných a . Pokud bychom znali hodnoty transformačních koeficientů , pak by řešení uvedené úlohy bylo v podstatě triviální. Avšak problém je, že tyto hodnoty dopředu neznáme. Znamená to, že výsledkem výpočtů vycházejících ze znalosti hodnot pozorovaných veličin musí být určení hodnot latentních veličin, ale i hodnot transformačních koeficientů. Takové řešení může vypadat jako naprosto nerealizovatelné. Bez jakýchkoliv dalších podmínek by se taková úloha opravdu řešit nedala. Zabývejme se tedy podmínkami, za kterých dokážeme řešení nalézt.

Pokusme se nyní výše uvedené jednoduché konkrétní zadání úlohy formulovat obecněji. Tedy předpokládejme, že máme k dispozici p-rozměrný náhodný vektor , jehož jednotlivé složky představují známá naměřená data. Nechť pro jednotlivé složky vektoru x platí

(2)

nebo také pomocí maticového zápisu

(3)

kde reprezentuje vektor původních (skrytých) zdrojových komponent a matice A je tzv. transformační matice. Hodnoty jejích prvků stejně jako hodnoty jednotlivých složek vektoru s primárně neznáme. Platí-li předpoklad, vyjádřený vztahy (2), resp. (3), můžeme také psát

(4)

což je ten vztah, který umožňuje ze známých hodnot vektoru určit neznámé složky vektoru latentních proměnných. Má-li být tento výpočet realizovatelný, musíme znát hodnoty prvků matice W, resp. A.