Fisherova lineární diskriminace

Fisherova lineární diskriminace je stejně jako Bayesův klasifikátor a lineární verze metody podpůrných vektorů  jednou z metod využívaných pro lineární klasifikaci dat. Pro základní vysvětlení podstaty této metody budeme uvažovat klasifikaci dvou tříd subjektů, a to pacientů a kontrol.

Principem Fisherovy lineární diskriminace je transformace do jednorozměrného (1-D) prostoru tak, abychom od sebe maximálně oddělili obě třídy (viz. Obr. 4). Je zřejmé, že pokud chceme od sebe dvě třídy separovat, měli bychom je promítnout tak, aby byly co nejdále od sebe, tzn., aby vzdálenost mezi jejich centroidy byla co největší. Ani velká vzdálenost centroidů však nemusí zaručit, že se po projekci nebudou lineárně separabilní třídy překrývat (viz projekce 1 v Obr. 4). Proto bychom měli vzít v úvahu i variabilitu uvnitř skupin, kterou chceme mít po projekci co nejmenší. Samotný požadavek na minimální variabilitu uvnitř skupin opět nemusí vést k úplnému oddělení lineárně separabilních tříd (viz projekce 2 v Obr. 4), proto se jeví jako vhodné použít kombinaci obou těchto požadavků.

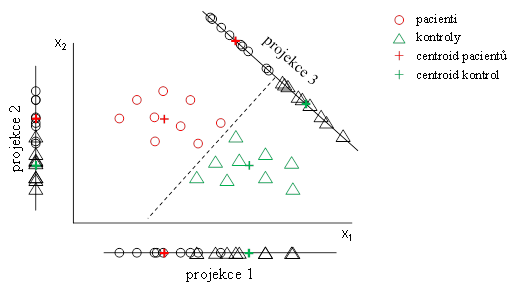
Obr. 4: Princip Fisherovy lineární diskriminace. Projekce 1 (tzn. projekce na osu ) umožňuje dosažení větší vzdálenosti centroidů než projekce 2 (tzn. projekce na osu ), zatímco projekce 2 umožňuje získání menší variability mezi skupinami než projekce 1. Ani jedna z těchto projekcí však neumožňuje dokonalé oddělení obou skupin, protože se skupiny při těchto projekcích překrývají. Dokonalé oddělení obou skupin získáme až při projekci 3, která maximalizuje vzdálenost mezi skupinami a současně minimalizuje variabilitu uvnitř skupin.Osy  a  odpovídají dvěma proměnným. Čárkovaná čára ukazuje hranici mezi oběma třídami, která je kolmá na nadrovinu, do níž promítáme.

 

Podstatou Fisherovy lineární diskriminace je tedy projekce do 1-D prostoru tak, abychom maximalizovali vzdálenost skupin (odráží se v čitateli Fisherova diskriminačního kritéria) a minimalizovali variabilitu uvnitř skupin (odráží se ve jmenovateli Fisherova diskriminačního kritéria). Fisherovo diskriminační kritérium je tedy ve tvaru:

(2)

kde  je projekce centroidu pacientů  do 1-D prostoru,  je projekce centroidu kontrol , je rozptyl uvnitř třídy pacientů po projekci do 1-D prostoru a  je rozptyl uvnitř třídy kontrol. Centroidy jsou vícerozměrné průměry pro třídu pacientů a kontrol:

(3)

kde  je hodnota první proměnné u -tého subjektu,  je počet proměnných,  je počet pacientů a  je počet kontrolních subjektů. Projekce centroidů do 1-D prostoru mohou být vypočítány jako  a , kde  je váhový vektor udávající směr 1-D prostoru, do něhož promítáme. Obecně může být průmět jakéhokoliv bodu  do 1-D prostoru vypočítán jako  a znázorněn pomocí Obr. 5.

Obr. 5: Znázornění projekce bodu  do 1-D prostoru daného směrovým vektorem w. Bod  
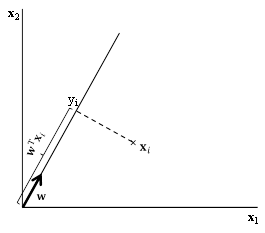
reprezentuje -tý subjekt a  je jeho projekce. Osy  a  odpovídají dvěma proměnným.

 

Rozptyl uvnitř třídy pacientů po projekci do 1-D prostoru ( ) lze vypočítat jako čtverec vzdáleností projekcí bodů odpovídajících jednotlivým pacientům od projekce centroidu:

 

(4)

kde  je kovarianční matice pacientů. Obdobně je možné rozptyl uvnitř třídy kontrol po projekci do 1-D prostoru ( ) vypočítat jako:

(5)

kde  je kovarianční matice kontrol.

Dále si rozepíšeme součet rozptylů uvnitř jednotlivých tříd po transformaci do 1-D prostoru, který se vyskytuje ve jmenovateli Fisherova diskriminačního kritéria:

(6)

kde  je suma čtverců variability uvnitř skupin a lze ji vypočítat jako: . V obecném případě, kdy nejsou vyvážené počty subjektů ve skupinách, se počítá vážená suma čtverců variability uvnitř skupin jako . Čitatel Fisherova diskriminačního kritéria si můžeme rozepsat jako:

(7)

 

kde  je suma čtverců variability mezi skupinami.

Fisherovo diskriminační kritérium tedy můžeme vyjádřit jako:

(8)

Chceme maximalizovat , proto  zderivujeme a položíme výraz roven 0:

(9)

 

Víme, že  má směr , protože , kde  je nějaký skalár. U vektoru  nás nezajímá jeho modul (tzn. velikost), jen jeho směr, proto můžeme pominout skalární členy  a . Dostáváme tedy:

(10)

z čehož můžeme vypočítat váhový vektor  jako:

(11)

Hranici mezi třídami lze pak vypočítat jako , kde  je průmět hraničního bodu v 1-D prostoru a lze ho spočítat pomocí vztahu .

Pokud chceme zařadit nějaký nový subjekt  do jedné z daných tříd, musíme nejprve vypočítat jeho průmět do 1-D prostoru   a tento průmět následně srovnat s průmětem hraničního bodu. Pokud  (přičemž ), subjekt zařadíme do skupiny kontrolních subjektů, jinak do skupiny pacientů.