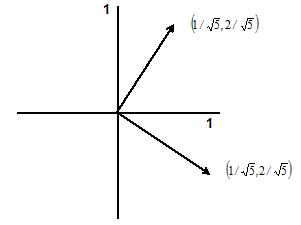Vlastní (charakteristická) čísla a vlastní (charakteristické) vektory matice

Pojem vlastních čísel a vlastních vektorů matice  vychází z její transformace na ekvivalentní diagonální matici , kde λ₁, λ₂, … λ_n jsou vlastní čísla matice A. Matice vlastních čísel je ekvivalentní s maticí A, pokud je možné matici A převést na matici pomocí elementárních operací popsaných v předchozí kapitole.

Vlastní čísla matice A spolu s jim odpovídajícími vlastními vektory se prakticky získávají řešením rovnice

(13)

kde u_j je sloupcový vlastní vektor. Rovnici (13) lze přepsat do tvaru

(14)

a dále po vytknutí u_j

(15)

kde I je jednotková matice. Kromě triviálního řešení, kdy je vektor u_j nulový, má charakteristická rovnice řešení dané vztahem

(16)

Tj. determinant rozdílu matic A a λ_j I musí být roven nule pro každé vlastní číslo λ_j. Tuto rovnici nazýváme charakteristickou rovnicí.

Pro matici A řádu n obsahuje charakteristická rovnice polynom n-tého stupně proměnné λ. Jejím řešením jsou hodnoty vlastních čísel. Pro známá vlastní čísla pak řešením soustavy rovnic (15) určíme ke každému známému vlastnímu číslu příslušný vlastní vektor.

Příklad Matice.22:

Určete vlastní čísla a jim příslušné vlastní vektory matice

Řešení:

Charakteristická rovnice má tvar

, tj. .

Rozvojem determinantu máme (2 – λ)(5 - λ) – 4 = 0, a tedy λ² - 7λ + 6 =0. Tato kvadratická rovnice má dvě řešení λ₁ = 6 a λ₂ = 1.

Z rovnice (15) pro každé vlastní číslo λ určíme vlastní vektory:

a to odpovídá soustavám dvou lineárních rovnic

Jak lze vidět z obou matic soustavy, resp. z obou rovnic, řádky v obou maticích soustav jsou lineárně závislé, proto mají obě soustavy rovnic nekonečné množství řešení. Vlastní vektory jsou všechny vektory z rovnic vyplývajících směrů. Abychom vybrali vždy jedno konkrétní řešení, zvolíme hodnotu jedné souřadnice vlastního vektoru a dopočítáme druhou.

Vlastní vektory zadané matice tedy mohou být:

pro λ₁ = 6 je  a pro λ₂ = 1 je . Protože jsme museli při určování vlastních vektorů vyřešit dříve zmíněnou neurčitost, jakékoliv vektory daného směru splňují podmínky na řešení obou soustav lineárních rovnic. Bývá často zvykem vlastní vektory normalizovat, aby jejich délka byla jednotková. Podle vztahu (Vektory 3) je pro normalizované vlastní vektory  a .

Protože zadaná matice A byla symetrická, jsou její vlastní vektory ortogonální, tj. jsou na sebe kolmé (Obr. 6). Podle kapitoly o vektorech platí pro dva kolmé vektory, že jejich skalární součin je roven nule.

Tedy ověřme: u₁.u₂ = 1.(-2) + 2.1 = 0.