Příklad
Bylo provedeno měření objemu hipokampu a mozkových komor (v cm3) u 3 pacientů se schizofrenií (
) a 3 kontrolních subjektů (
) (označení D – diseased, H – healthy). Naměřené hodnoty objemu hipokampu a mozkových komor u pacientů ( 
resp. 
) a kontrol ( 
resp. 
) byly zaznamenány do matic resp. :
Určete, zda testovací subjekt 
patří do skupiny pacientů či kontrolních subjektů pomocí Fisherovy lineární diskriminace.
Řešení
Pro výpočet váhového vektoru 
, který udává směr nadroviny, do níž budeme promítat a jež je kolmá na hranici oddělující obě skupiny, budeme potřebovat spočítat centroidy (vícerozměrné průměry) pro třídu pacientů (
) a kontrol (
) a rovněž sumu čtverců variability mezi skupinami ( 
) včetně její inverze. Pro výpočet matice využijeme výběrové kovarianční matice pro třídu pacientů (
) a kontrol (
). Centroidy a kovarianční matice jsou následující: 
, 
, 
a 
(detailní výpočet centroidů a výběrových kovariančních matic je uveden v řešení příkladu v podkapitole Klasifikace pomocí diskriminačních funkcí). Suma čtverců variability mezi skupinami bude tedy spočítána jako 
a její inverze jako 
.
Váhový vektor poté tedy můžeme spočítat následujícím způsobem:
Protože nás nezajímá modul váhového vektoru, ale jen jeho směr, můžeme váhový vektor přeškálovat na: 
. Nyní můžeme vypočítat průměty centroidů do 1-D prostoru:
A následně vypočteme průmět hraničního bodu do 1-D prostoru 
:
Hraniční bod lze vypočítat i takto:
(protože jsme váhový vektor přeškálovali pomocí vynásobení šesti, musíme vynásobit šesti i a pak získáváme 13,5).
Pokud chceme zařadit nový subjekt do jedné z daných tříd, musíme nejprve vypočítat jeho průmět do 1-D prostoru:
Průmět následně srovnáme s hraničním bodem: protože 
, subjekt zařadíme do skupiny pacientů (pacienti leží napravo od hraničního bodu, protože centroid pacientů má větší hodnotu než hraniční bod).
Po výpočtu váhového vektoru a hraničního bodu můžeme určit obecnou rovnici hranice (normálou hraniční přímky je váhový vektor ):
Pro vykreslení hranice je vhodné vyjádřit hranici ve tvaru 
:
Nová osa, do níž se promítá, má směr odpovídající váhovému vektoru (je kolmá k hranici) a prochází počátkem a lze ji tedy vyjádřit obecnou rovnicí jako:
Pokud nás zajímají souřadnice hraničního bodu 
v původním prostoru, využijeme znalosti, že hraniční bod je průsečík hranice a nové osy:
---------------------------------------
--------------------------------------
Souřadnici 
pak vypočítáme z první rovnice jako 
:
Souřadnice hraničního bodu v původním prostoru jsou tedy 
:
Ověření, že po projekci hraničního bodu dostanu hodnotu 13,5: 
Klasifikaci pomocí Fisherovy lineární diskriminační analýzy si na závěr znázorníme pomocí Obr. 6.
Obr. 6. Znázornění klasifikace pomocí Fisherovy lineární diskriminační analýzy. Klasifikační hranice je znázorněna tmavě modře, nová osa, do níž se promítá, světle modře a hraniční bod je vyznačen tmavě modrým prázdným kolečkem. Původní osy a odpovídající dvěma proměnným (objemu hipokampu a mozkových komor) jsou znázorněny čárkovanými čarami.
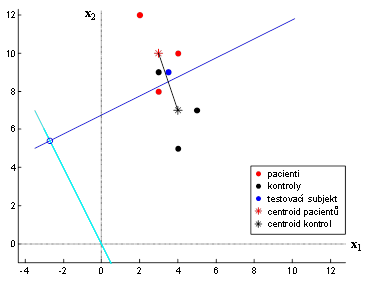
Poznámka: Pokud bychom váhový vektor znormovali, hraniční bod 
by přímo ležel ve vzdálenosti od počátku:
(tzn. hraniční bod leží ve vzdálenosti 6,04 od počátku v původních souřadnicích).
