Můžeme konstatovat, že všechny řádky i sloupce libovolné matice reprezentují vektory. Vektorem tedy také můžeme nazvat matici s jedním jednotkovým rozměrem. V tom případě je a = A_1,m řádkovým vektorem s m složkami a b = B_n,1 sloupcovým vektorem s n složkami.

Jak už bylo naznačeno v úvodní kapitole, prvky matice při řešení praktických úloh bývají naměřené či jinak zjištěné hodnoty veličin popisujících objekty daného typu. Je formálním zvykem tyto údaje uspořádat tak, že řádky v matici odpovídají jednotlivým analyzovaným objektům (pacient, lokalita, experiment, …) a sloupce jednotlivým veličinám, proměnným, znakům (výška, hmotnost, pohlaví, koncentrace cholesterolu, kuřák/nekuřák, …). Reálná data tedy bývají uspořádána do matice ve tvaru podle Obr.4.

Obr.4: Struktura datové matice

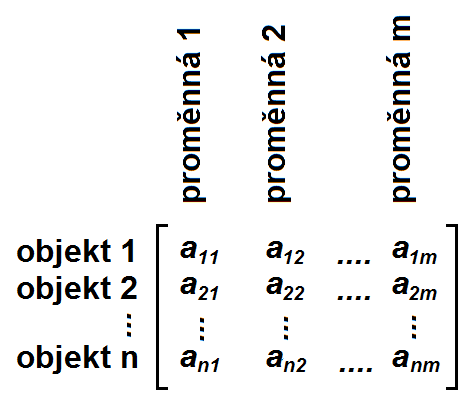
Příklad Matice.1

Předpokládejme skupinu 3 pacientů, z nichž každý je popsán v uvedeném pořadí následujícími údaji: věk v letech, výška v cm, hmotnost v kg, pohlaví, hodnota systolického krevního tlaku v mmHg a hodnota diastolického tlaku v mmHg. Datovou matici pak můžeme zapsat ve tvaru (při binárním kódování pohlaví muž – 0, žena – 1)

Jak je vysoká žena v uvedené skupině pacientů? Zdůvodněte proč.

Skryté řešení:

165 cm, protože je to hodnota ve druhém sloupci (odpovídajícímu výšce pacientů) v jediném řádku s hodnotou 1 (ženské pohlaví) ve 4. sloupci.

Vysvětlení pojmu Matice.2

Prvky matice a_ii (i = 1, …, min(n,m)) tvoří hlavní diagonálu matice A, prvky a_i,m-i+1 (i = 1, …, min(n,m)) jsou prvky tzv. vedlejší diagonály matice A.

a)	b)
Obr.5: Příklady diagonálních prvků matice – a) matice s nenulovými prvky hlavní diagonály; b) matice s nenulovými prvky vedlejší diagonály

Příklad Matice.2

V matici D_3,5 v příkladu 3.1 tvoří hlavní diagonálu prvky 26, 192 a 102, prvky vedlejší diagonály jsou 75, 135 a 0.

Vysvětlení pojmu Matice.3

Matice s týmž počtem řádků a sloupců, tj. n = m, nazýváme čtvercovou matici n-tého stupně.

Příklad Matice.3

Matice je čtvercová matice.

Vysvětlení pojmu Matice.4

Matice 0, jejíž všechny prvky jsou nulové, se nazývá nulová matice.

Příklad Matice.4

Matice je nulová matice.

Vysvětlení pojmu Matice.5

Čtvercovou matici, jejíž všechny prvky ležící mimo hlavní diagonálu jsou nulové, nazýváme diagonální matice.

Příklad Matice.5

Matice je diagonální matice.

Vysvětlení pojmu Matice.6

Diagonální matici I, jejíž všechny prvky na hlavní diagonále jsou rovny jedné, nazýváme jednotková matice.

Poznámka:

Zatímco nulová matice 0 je neutrální z hlediska sčítání (součet matice A s nulovou maticí 0 je roven matici A), jednotková matice I je neutrální z hlediska násobení. Tedy součin matice A s jednotkovou maticí je roven matici A. Obě skutečnosti vyplynou po zavedení základních operací s maticemi.

Vysvětlení pojmu Matice.7

Čtvercovou matici, jejíž všechny prvky pod nebo nad hlavní diagonálou jsou nulové, nazýváme trojúhelníkovou (triangulární) maticí. Pokud se nulové prvky trojúhelníkové matice nacházejí ve všech prvcích matice pod hlavní diagonálou (ty obecně nenulové jsou nad hlavní diagonálou), nazýváme tuto matici horní trojúhelníkovou.

Příklad Matice.6

Ekvivalentně ke způsobu popisu horní trojúhelníkové matice se pokuste zavést pojem dolní trojúhelníková matice.

Řešení:

Pokud se nulové prvky trojúhelníkové matice nacházejí ve všech prvcích matice nad hlavní diagonálou (ty obecně nenulové jsou pod hlavní diagonálou), nazýváme tuto matici dolní trojúhelníkovou.

Příklad Matice.7

Matice je trojúhelníková matice.