Centroidová metoda

Je představitelkou metod, které určují vzdálenost mezi množinami pomocí vzdálenosti jejich reprezentativních vektorů. Takovým vektorem může být tzv. centroid, což je vektor, který je určený průměrem, mediánem, resp. jinou významnou charakteristikou, vyjadřující nějakou souhrnnou vlastnost všech vektorů dané množiny. Zatímco centroid je nový, uměle spočítaný vektor reprezentující množinu, tzv. medoid je jeden z vektorů dané množiny, který má optimální vlastnost z hlediska nějaké souhrnné charakteristiky, např. vektor, jehož vzdálenost od všech ostatních vektorů množiny je minimální.

V případě centroidu v euklidovském p-rozměrném prostoru je vzdálenost dvou shluků určena euklidovskou vzdáleností mezi centroidy, reprezentujícími obě množiny.

Je-li např. centroid definován pomocí středních hodnot souřadnic všech vektorů patřících do dané množiny, tj. představuje-li

reprezentativní vektor (centroid) množiny C _i, kde

pak

Nevýhodou centroidové metody je skutečnost, že v případě spojování dvou shluků velmi rozdílné velikosti bude centroid (těžiště) nového shluku velmi blízko většího shluku (nebo dokonce uvnitř). Vlastnosti menšího shluku se tak do jisté míry ztrácejí (Obr. 7).

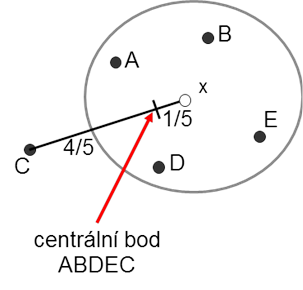
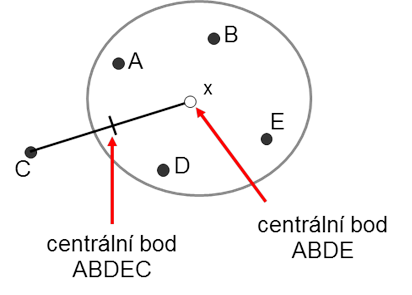
Z toho důvodu se občas používá vážená centroidová metoda, která odstraňuje problém daný rozdílnou velikostí spojovaných shluků. Analyzované shluky se považují za stejně velké a tedy se stejnou vahou při výpočtu, centroid nového shluku je proto vždy v polovině vzdálenosti mezi centroidy spojovaných shluků (Obr. 8). To znamená, že nový centroid získáme jako nevážený průměr původních centroidů. Jde ovšem o vážený průměr ze všech bodů nového shluku. Tato metoda je preferována tehdy, když očekáváme velké rozdíly ve velikosti shluků.

Příklad 7.7

Předpokládejme opět vektory vektory  = (0, 0),  = (10, 10),   = (8, 8),   = (6, 7),  = (4, 3) a  = (3, 2) rozdělené do dvou množin = {x₁, x₅, x₆} a = {x₂, x₃, x₄}. Jaká je vzdálenost obou množin podle centroidové metody, přičemž centroidy obou množin nechť jsou určeny středními hodnotami souřadnic vektorů. Výslednou vzdálenost mezi centroidy určujeme znovu pomocí Hammingovy metriky.

Řešení:

Střední hodnota souřadnic vektorů první množiny jsou  a  a druhé množiny  a . Centroidy obou množin v tom případě jsou  a  a jejich Hammingova vzdálenost je .