
Analýza rozptylu pro vícerozměrná data
V této podkapitole si představíme rozšíření jednorozměrné analýzy rozptylu (ANOVA) pro vícerozměrná data. Pokud zkoumáme vliv jediného faktoru (kategoriální proměnné) na jednu či více vysvětlovaných spojitých proměnných, mluvíme o analýze rozptylu jednoduchého třídění (neboli jednofaktorové analýze rozptylu). Při větším počtu faktorů se jedná o analýzu rozptylu dvojného, trojného apod. třídění (tedy o vícefaktorovou analýzu rozptylu), přičemž se faktory mohou ovlivňovat (model s interakcí) či se ovlivňovat nemusejí (model bez interakce). V případě, že je vysvětlovaná proměnná pouze jedna, hovoříme o jednorozměrné analýze rozptylu (ANOVA), zatímco při zkoumání vlivu jednoho či více faktorů na více vysvětlovaných proměnných mluvíme o vícerozměrné analýze rozptylu (MANOVA). Pro větší názornost si uveďme několik příkladů různých typů úloh:
- zkoumáme dlouhodobý vliv třech typů léků na hodnoty systolického tlaku u skupiny osob – jedná se o jednorozměrnou analýzu rozptylu jednoduchého třídění;
- zkoumáme dlouhodobý vliv třech typů léků na hodnoty systolického tlaku u skupiny osob, přičemž chceme zkoumat i vliv pohlaví, předpokládáme však, že ženy i muži reagují na jednotlivé léky obdobně (tzn. např. ženy s léky A a C budou mít nižší tlak než ženy s lékem B a muži s léky A a C budou mít také nižší tlak než muži s lékem B apod.) – jedná se o jednorozměrnou analýzu rozptylu dvojného třídění bez interakce;
- zkoumáme dlouhodobý vliv třech typů léků na hodnoty systolického tlaku u skupiny osob, přičemž chceme zkoumat i vliv pohlaví, a předpokládáme, že ženy a muži budou reagovat na léky různě (tzn. např. ženy s léky A a C budou mít nižší tlak než ženy s lékem B, zatímco muži s léky A a C budou mít vyšší tlak než muži s lékem B apod.) – jedná se o jednorozměrnou analýzu rozptylu dvojného třídění s interakcí;
- zkoumáme dlouhodobý vliv třech typů léků na hodnoty systolického a diastolického tlaku u skupiny osob – jedná se o vícerozměrnou analýzu rozptylu jednoduchého třídění;
- zkoumáme dlouhodobý vliv třech typů léků a vliv pohlaví na hodnoty systolického a diastolického tlaku u skupiny osob – jedná se o vícerozměrnou analýzu rozptylu dvojného třídění.
Začněme nejprve stručným popisem jednorozměrné analýzy rozptylu jednoduchého třídění, kdy srovnáváme tři a více skupin dat, které jsou na sobě nezávislé. Předpokladem je normalita dat ve všech skupinách a shodnost (homogenita) rozptylů všech srovnávaných skupin. Principem je srovnání variability mezi výběry s variabilitou uvnitř výběrů
(Obr. 3), které můžeme vypočítat jako
|
(4)
|
|
|
(5)
|
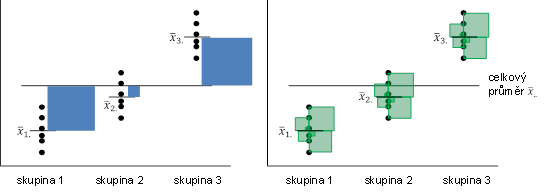
Obr. 3. Ilustrace výpočtu variability mezi výběry (vlevo) a variability uvnitř výběrů (vpravo).
Můžeme vypočítat také celkový součet čtverců
|
(6)
|
Výsledky zapíšeme do tzv. tabulky analýzy rozptylu (Tabulka 1), kde n je celkový počet subjektů a
je výsledná p-hodnota. Pokud
, zamítáme nulovou hypotézu o shodě středních hodnot jednotlivých skupin subjektů
.
Tabulka 1. Tabulka jednorozměrné analýzy rozptylu jednoduchého třídění.
Využijeme nyní skutečnosti, že model analýzy rozptylu je speciálním případem obecného lineárního modelu, můžeme tedy jednorozměrnou analýzu rozptylu jednoduchého třídění zapsat jako lineární model následujícím způsobem:
|
(7)
|
kde je celkový průměr,
je i-tý efekt faktoru A a
je reziduum. Nulovou hypotézu lze pak vyjádřit jako
. Rozšířením tohoto modelu můžeme definovat další modely analýzy rozptylu pro více faktorů, hodnocení interakcí, opakovaná měření na jednom subjektu apod.




