
Příbuzná rozdělení pravděpodobnosti
Na závěr kapitoly o zákonu malých čísel ještě krátce uvedeme další rozdělení pravděpodobnosti, která jsou principiálně spjata s Poissonovým rozdělením a jež budeme v dalších částech používat. Nechť je náhodná veličina nabývající hodnot v intervalu
a to s hustotou pravděpodobnosti (probability density function)
|
|
kde je dané číslo. Potom říkáme, že náhodná veličina
má exponenciální rozdělení pravděpodobnosti s parametrem
. Později uvidíme, exponenciální rozdělení popisuje časové intervaly mezi příchody tzv. řídkých událostí, tedy takových, jejichž výskyt je popsán zákonem malých čísel (Poissonovým rozdělením) (4). V našem výkladu budeme o veličině
hovořit jako o čase. Jak uvidíme ze vztahu pro střední hodnotu, parametr
má potom rozměr rovný převrácené hodnotě času.
Distribuční funkce, exponenciálního rozdělení je rovna
|
|
Zobecněním exponenciálního rozdělení je tzv. gama rozdělení, které ve speciálním případě dostáváme součtem nezávislých exponenciálně rozdělených náhodných veličin se stejným parametrem
. Náhodná veličina
spojitého typu má gama rozdělení s parametry
a
, když má hustotu pravděpodobnosti
|
|
Přitom je tzv. gama funkce, pro
daná určitým integrálem
|
|
Bezrozměrný parametr se někdy nazývá parametrem tvaru. Pro
platí vztah
, odpovídající rozdělení pravděpodobnosti se též nazývají Erlangova rozdělení. Speciálním případem gama rozdělení je již zmíněné exponenciální rozdělení, které dostaneme volbou
. Pro Erlangova rozdělení (
), lze distribuční funkci napsat ve tvaru
|
|
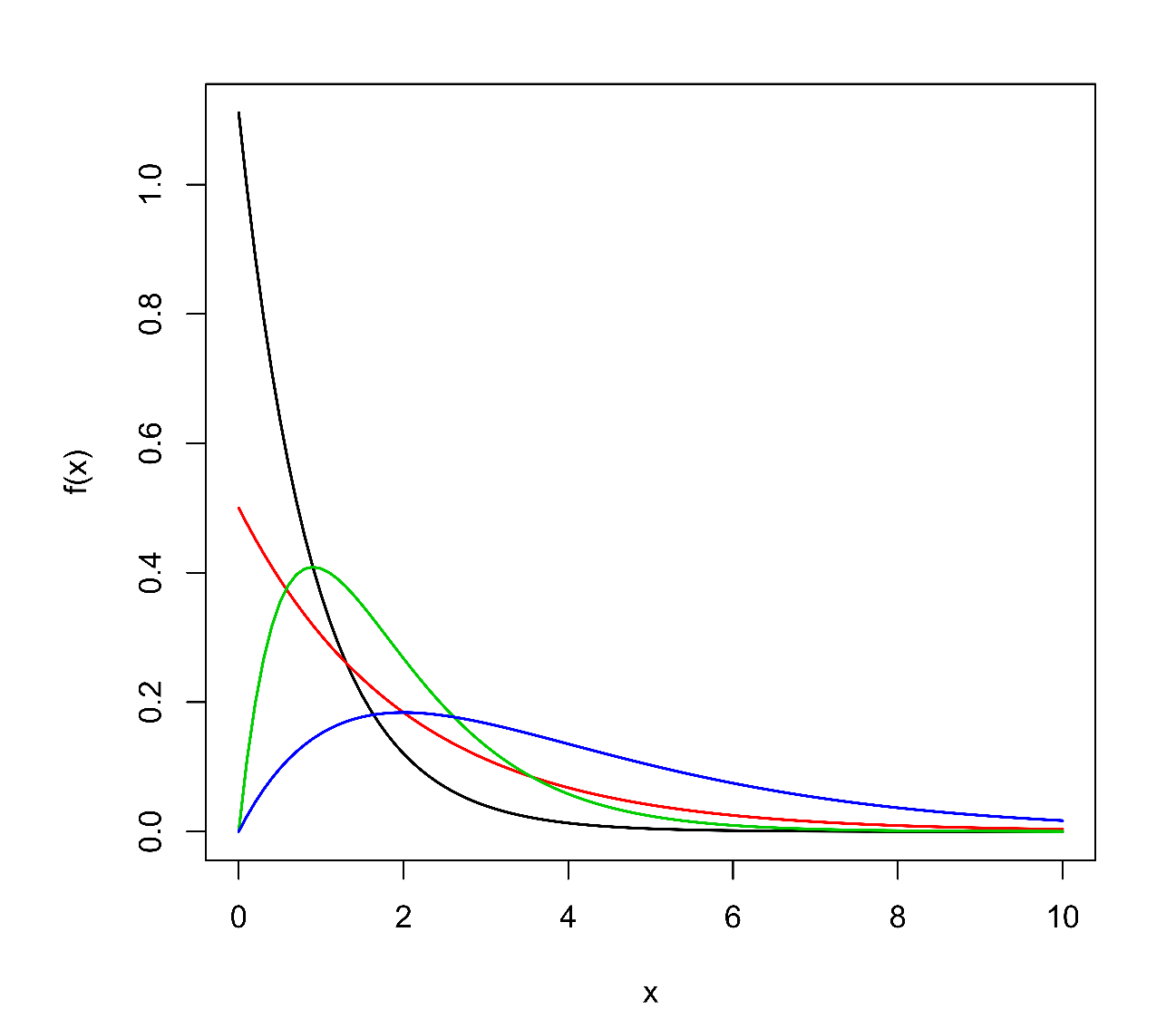
Grafy hustot a odpovídajících distribučních funkcí
jsou pro některé hodnoty parametrů
zobrazeny na Obr. 4. Pro
je hustota ryze klesající a distribuční funkce konvexní. Pro
nabývá hustota lokálního maxima pro
(tzv. mod), odpovídající distribuční funkce zde má inflexní bod.
 |
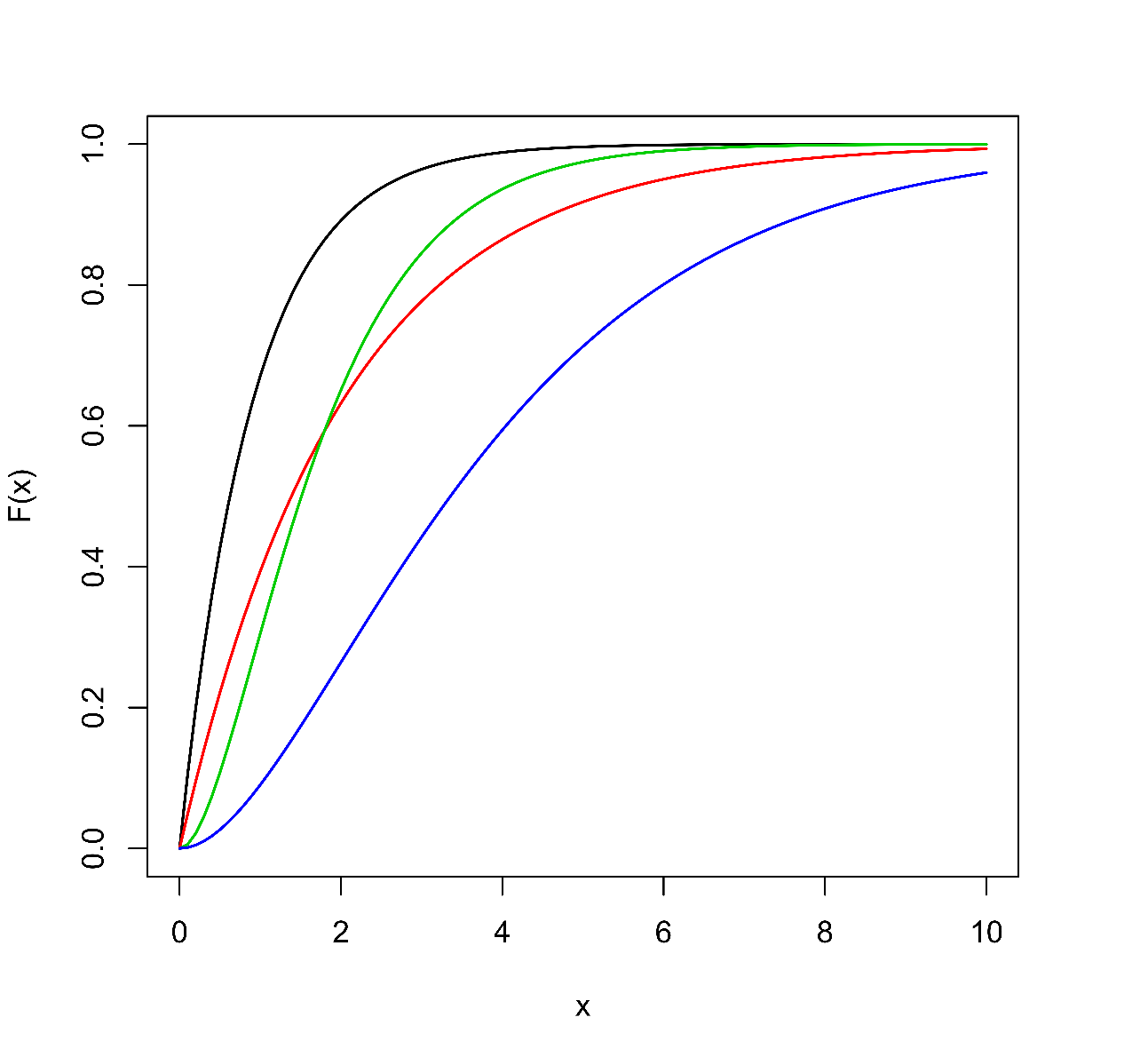 |
Obr. 4: Hustoty pravděpodobnosti a odpovídající distribuční funkce gama rozdělení pravděpodobnosti. Parametry mají hodnoty: (černě);
(červeně);
(zeleně);
(modře). V případech
se jedná o exponenciální rozdělení.
Střední hodnota a rozptyl gama rozdělení jsou rovny
|
|
|
|
|
Pro exponenciální rozdělení, tzn. když , si všimněme typického znaku, kdy rozptyl je roven kvadrátu střední hodnoty,
.




