Yuleův proces

Yuleův proces (ve fyzice nazýván též Yuleův-Furryův proces) je jednoduchý stochastický proces, který navrhl britský statistik George Udny Yule (1871-1951) v roce 1924 jako model vzniku nových druhů organismů. Jeho reálné využití jako model populačního růstu je dosti omezeno, např. na modely růstu řas ve velkých jezerech, avšak je skvělým příkladem, jak matematicky popsat i složitější situace podobného typu. Předpoklady Yuleova procesu jsou následující:

(a)	narození potomka se u každého jedince vyskytuje nezávisle na ostatních jedincích;
(b)	pravděpodobnost narození jednoho potomka v krátkém časovém intervalu délky  je pro každého jedince rovna , pravděpodobnost nenarození potomka je rovna , a pravděpodobnost narození více než jednoho potomka je ;
(c)	neuvažují se úmrtí, jedinci přežívají nekonečně dlouho a stále jsou schopni reprodukce.

Parametr vyjadřuje střední počet narozených potomků pro každého jedince za jednotku času. Označme velikost populace v čase a nechť . Za podmínek (a) a (b) je počet narození v celé populaci za časový interval náhodnou veličinou s binomickým rozdělením pravděpodobnosti s opakováními a pravděpodobností úspěchu . Z pravděpodobnostní funkce (Zákon malých čísel 1) tohoto rozdělení pak pro dostáváme

Yuleův proces je tedy definován vlastnostmi:

(i)
(ii)
(iii)

Pro Yuleův proces nyní odvodíme pravděpodobnostní funkci velikosti populace v čase . Předpokládejme, že na začátku pozorování je velikost populace rovna , a označme hledanou pravděpodobnostní funkci . Podle pravidla o celkové pravděpodobnosti a pomocí vlastností (a) a (b) rozepíšeme

což po dosazení z (i) a (ii) dává pro vztah

(1)

Pro je vyloučeno narození potomka a vztah se tedy zjednoduší na

(2)

Dále převedeme výrazu , resp. , v (1), resp. (2), na levou stranu, vyděleníme a limitním přechodem obdržíme diferenciální rovnice

	(3)
	(4)

Řešením systému (3), (4) jsou pravděpodobnostní funkce

(5)

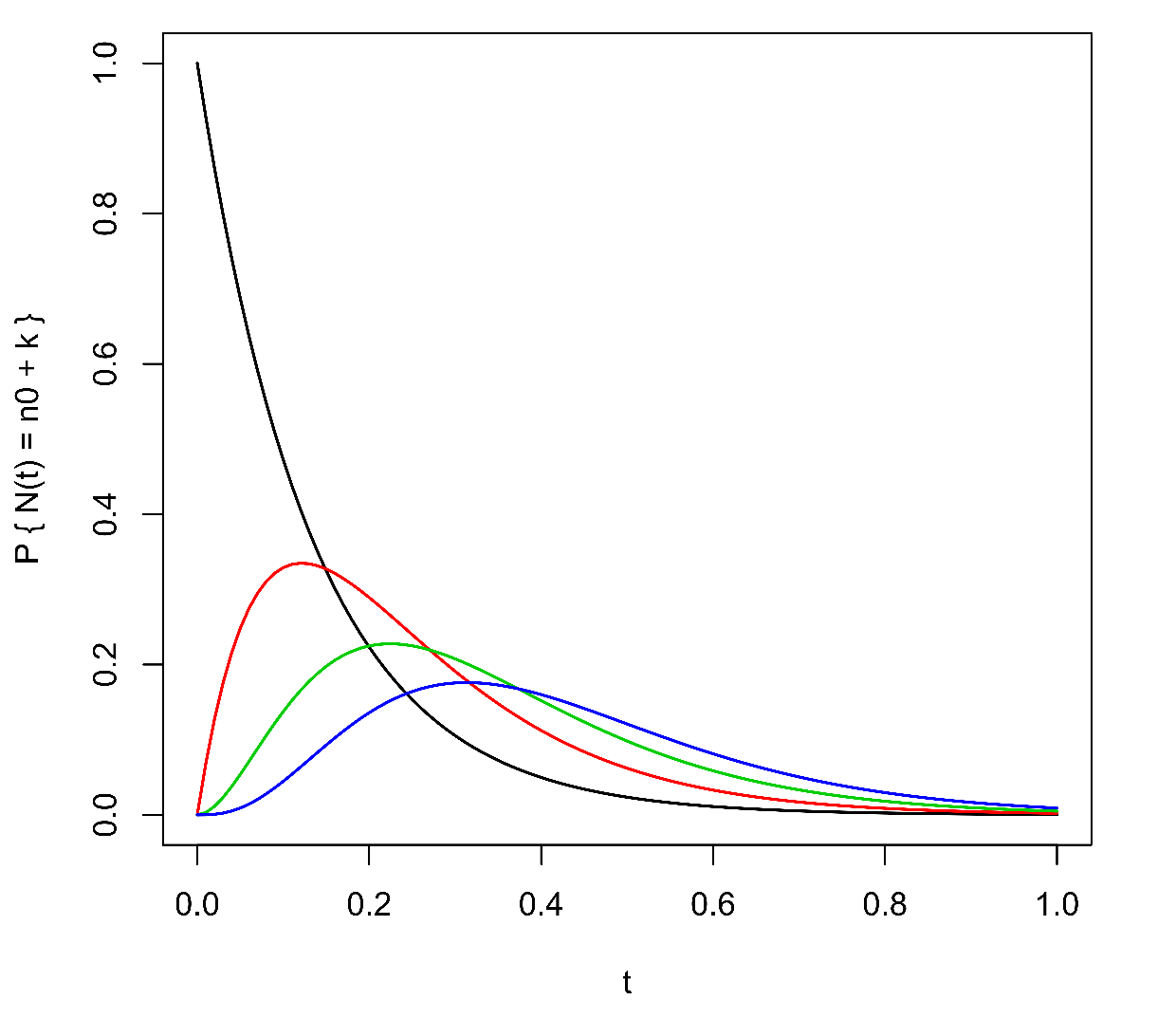
Grafy průběhu těchto funkcí pro některá v závislosti na čase jsou nakresleny na Obr.1 vlevo. Pro pravděpodobnostní funkce exponenciálně klesá z hodnoty 1 k nule, pro funkce začínají v bodě 0, nabývají lokálních maxim v časech a poté klesají k nule.

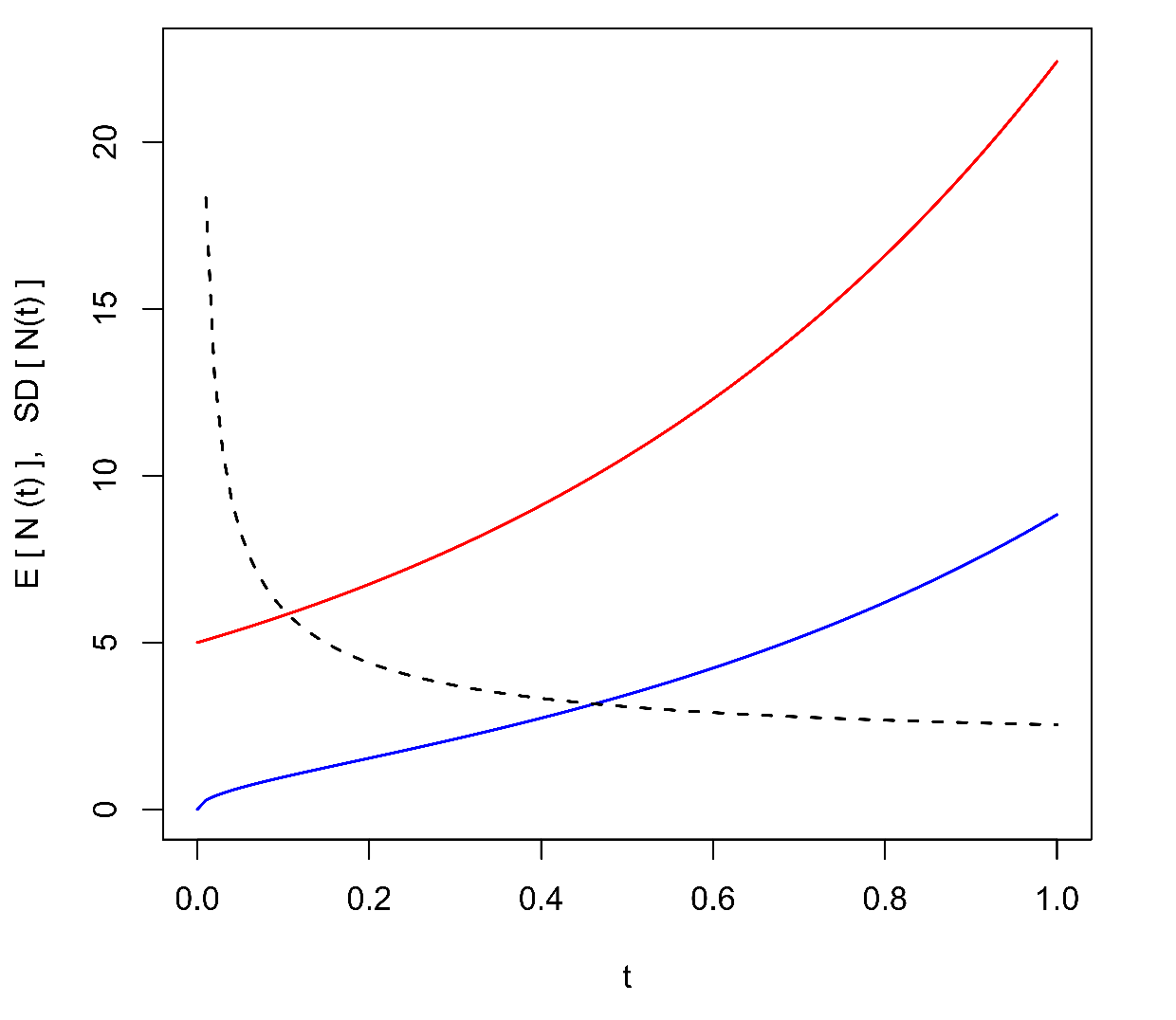
Obr.1: Vlevo: pravděpodobnostní funkce (5) Yuleova procesu jako funkce času, , pro velikosti populace (černě), (červeně), (zeleně) a  (modře). Vpravo: střední hodnota (červeně) a směrodatná odchylka (modře) velikosti populace a jejich poměr (čárkovaně černě) v čase. Parametr , počáteční velikost populace byla .

Negativně binomické rozdělení pravděpodobnosti

Pojem negativně binomického rozdělení pravděpodobnosti se v různých textech mírně liší. My jej zde zavedeme v následující podobě. Uvažujme posloupnost bernoulliovských pokusů s pravděpodobností úspěchu , podobně jako při definici binomického rozdělení. Náhodnou veličinou označíme počet pokusů potřebných k dosažení -tého úspěchu, , a to včetně tohoto úspěchu. Ze znalosti binomického rozdělení lehce spočítáme, že 

(6)

Rozdělení pravděpodobnosti náhodné veličiny se nazývá negativně binomické s parametry a . Přímým výpočtem z výše uvedené pravděpodobnostní funkce lze ukázat, že střední hodnota a rozptyl tohoto rozdělení jsou rovny

	(7)
	(8)

Vraťme se nyní k pravděpodobnostní funkci (5) velikosti populace v Yuleově procesu a porovnejme ji s (6). Vidíme, že velikost populace má negativně binomické rozdělení s parametry a . Využijeme toho k výpočtu střední hodnoty a rozptylu velikosti populace v čase ,

	(9)
	(10)

Pro se rozptyl asymptoticky chová jako funkce , tedy směrodatná odchylka velikosti populace je přibližně tvaru . Střední hodnota i směrodatná odchylka velikosti populace tedy sice rostou, jejich poměr však pro velká zůstává konstantní, rovný . Průbehy střední hodnoty (9) a směrodatné odchylky (odmocniny z (10)) jsou nakresleny na (Obr.1) vpravo.