Číselné charakteristiky a rozdělení pravděpodobnosti

Střední hodnotu a rozptyl náhodné procházky můžeme odvodit i bez znalosti rozdělení pravděpodobnosti náhodné veličiny , použijeme jen definici náhodné procházky a vlastnosti alternativního rozdělení pravděpodobnosti. Připomeňme, že jsou nsr náhodné veličiny, mají tedy i stejné číselné charakteristiky. Využijeme (iii) a střední hodnotu náhodné procházky zapíšeme ve tvaru

Střední hodnoty na pravé straně lehce spočítáme a dostaneme

(2)

Dále spočítáme druhý moment náhodné veličiny ,

a následně její rozptyl,

Odtud, s využitím nezávislosti a (iii) spočítáme rozptyl náhodné procházky,

(3)

Vidíme, že střední hodnota i rozptyl náhodné procházky rostou lineárně s počtem kroků , směrodatná odchylka má (řádově) tvar odmocniny .

Tyto vztahy a skutečnost, že poloha náhodné procházky po krocích je dle (ii) a (iii) dána součtem nsr náhodných veličin, nám umožní odvodit přibližné pravděpodobnostní rozdělení polohy náhodné procházky pro velká . Centrální limitní věta říká, že rozdělení pravděpodobnosti takového součtu náhodných veličin konverguje pro ke standardizovanému normálnímu rozdělení pravděpodobnosti, 

Konkrétně, po dosazení (2) a (3) dostáváme

(4)

Toho můžeme využít například pro konstrukci přibližného intervalu spolehlivosti. % interval spolehlivosti pro hodnotu jednoduché náhodné procházky je pro velká přibližně rovný

(5)

kde označuje % kvantil rozdělení . Střední hodnota (2) a intervalů spolehlivosti (5) jako funkce jsou vykresleny na Obr.2. Meze intervalů spolehlivosti mají (řádově) tvar funkcí posunutých o střední hodnotu (která má tvar lineární funkce).

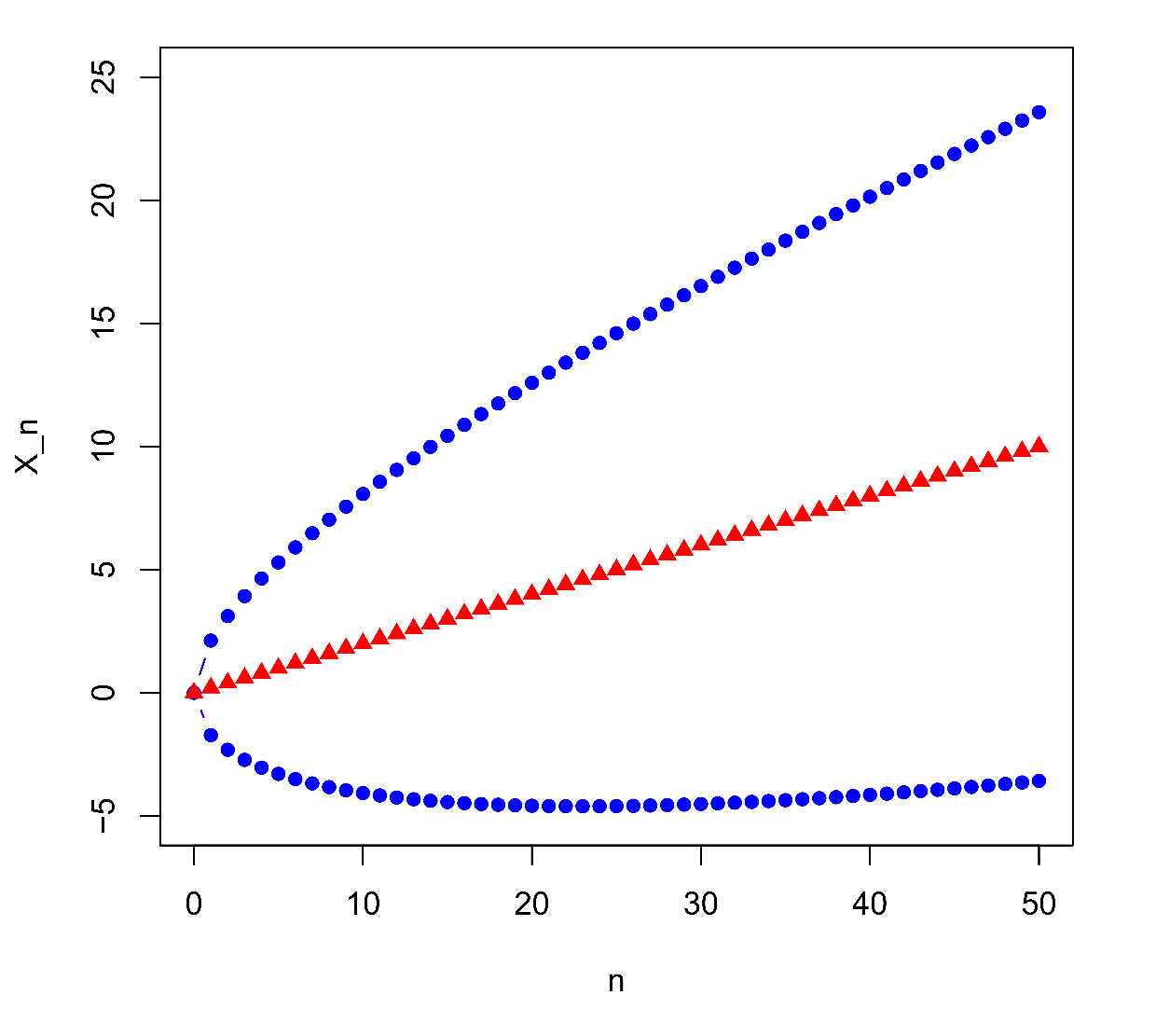Obr.2: Střední hodnota (červené trojúhelníky) dle (2) a přibližné 95% intervaly spolehlivosti (5) (meze určené modrými kolečky) pro hodnotu jednoduché náhodné procházky s p = 0,6 .

Rozdělení pravděpodobnosti pro libovolné

Nyní odvodíme rozdělení pravděpodobnosti polohy jednoduché náhodné procházky, , , po krocích. K tomu abychom se po krocích dostali do polohy potřebujeme alespoň kroků. Tedy pro .

Dále proto uvažujme pouze a označme jako náhodnou veličinu počet těch kroků , které mají hodnotu  . Počet kroků , které mají hodnotu  , je pak zřejmě rovný a dle (iii) můžeme psát

(6)

Jev tedy podle (6)  nastane právě tehdy, když

(7)

přičemž a musí být buď obě lichá, anebo obě sudá. Současně z (ii) víme, že má binomické rozdělení (Zákon malých čísel 1) s parametry a . Dospěli jsme tedy k rozdělení pravděpodobnosti náhodné procházky po krocích,

(8)

pro , a , obě lichá, anebo obě sudá.