Proces vzniku a zániku

Proces vzniku a zániku (birth and death process) je kombinací Yuleova procesu a procesu ryzího zániku. Opět označme velikost populace v čase a nechť . Každý jedinec bude mít během krátkého intervalu jednoho potomka s pravděpodobností , nebo může během této doby zemřít
s pravděpodobností. Přitom narození potomků jednotlivým jedincům, resp. jejich úmrtí, jsou nezávislá. Z těchto vlastností vychází matematické podmínky, kterými je proces vzniku a zániku definován:

(i*)
(ii*)
(iii*)

Tyto podmínky navíc implikují, že 

(iv*)

Pomocí pravidla o úplné pravděpodobnosti sestavíme systém diferenčních rovnic pro pravděpodobnostní funkce velikosti populace v čase , přičemž . Podle pravidel (i*) - (iv*) je možno populace velikosti   dosáhnout jen v případech, kdy, tedy 

Limitním přechodem přejdeme k systému diferenciálních rovnic 

(18)

pro _, spolu s první rovnicí 

(19)

a s počátečními podmínkami a pro . Tento systém diferenciálních rovnic však, narozdíl od systémů pro Yuleův proces, Poissonův proces či proces ryzího zániku, nelze vyřešit analyticky a v praxi se musí řešit některou z numerických metod.
Bez odvození tak uvedeme pravděpodobnost vyhynutí populace (kdykoliv v průběhu svého vývoje), 

>

(20)

Jinak řečeno, vyhynutí populace je nevyhnutelné, pokud je porodnost menší nebo stejně velká jako úmrtnost. Jako překvapivé se může zdát, že vyhynutí je nevyhnutelné i při rovnosti porodnosti a úmrtnosti. Je to způsobeno tím, že jev je v konečné vzdálenosti od aktuální hodnoty a tedy dosažitelný. Nicméně, pro je očekávaný čas do vyhynutí populace nekonečný, zatímco při je konečný. 

Na závěr odvodíme střední hodnotu a rozptyl velikosti populace v čase . Odvození je netypické tím, že požadované číselné charakteristiky odvodíme i přesto, že nemáme analyticky odvozený tvar pravděpodobnostních funkcí, ale jen systém diferenciálních rovnic (18), (19). Označme střední hodnotu procesu vzniku a zániku . Z definice střední hodnoty máme 

Rovnici derivujeme podle času, 

a do sumy na pravé straně dosadíme pravé strany (18), (19), čímž dostaneme 

Závorku uvnitř sumy roznásobíme a pomocí identit 

rozepíšeme první a poslední člen na dvě sumy; celkově tedy na pravé straně bude pět sum. V prvních dvou sumách posuneme sčítací index a v posledních dvou sumách podobně, . Tím dostane tvar 

Součet první, třetí a čtvrté sumy, tedy těch, obsahujících výraz , je rovný takže po dosazení zůstane 

Výraz a nulový člen pro vložíme do poslední sumy, 

Suma na pravé straně je opět střední hodnotou . Sestavili jsme tak diferenciální rovnici pro neznámou střední hodnotu, , 

(21)

s počáteční podmínkou . Řešením této úlohy je funkce 

(22)

Vidíme, že je konstantní, rovna , pro , exponenciálně klesá k nule pro , a exponenciálně roste nade všechny meze, pokud . 

Označme dále druhý obecný moment velikosti populace v čase . Analogicky odvození střední hodnoty lze ukázat, že tato funkce splňuje diferenciální rovnici 

(23)

s počáteční podmínkou . Pomocí řešení této počáteční úlohy potom odvodíme rozptyl , 

(24)

Rozptyl tedy s rostoucím čase roste exponenciálně, resp. ve speciálním případě roste lineárně. Časové průběhy střední hodnoty (22) a směrodatné odchylky z (24) jsou vykresleny na Obr.3.

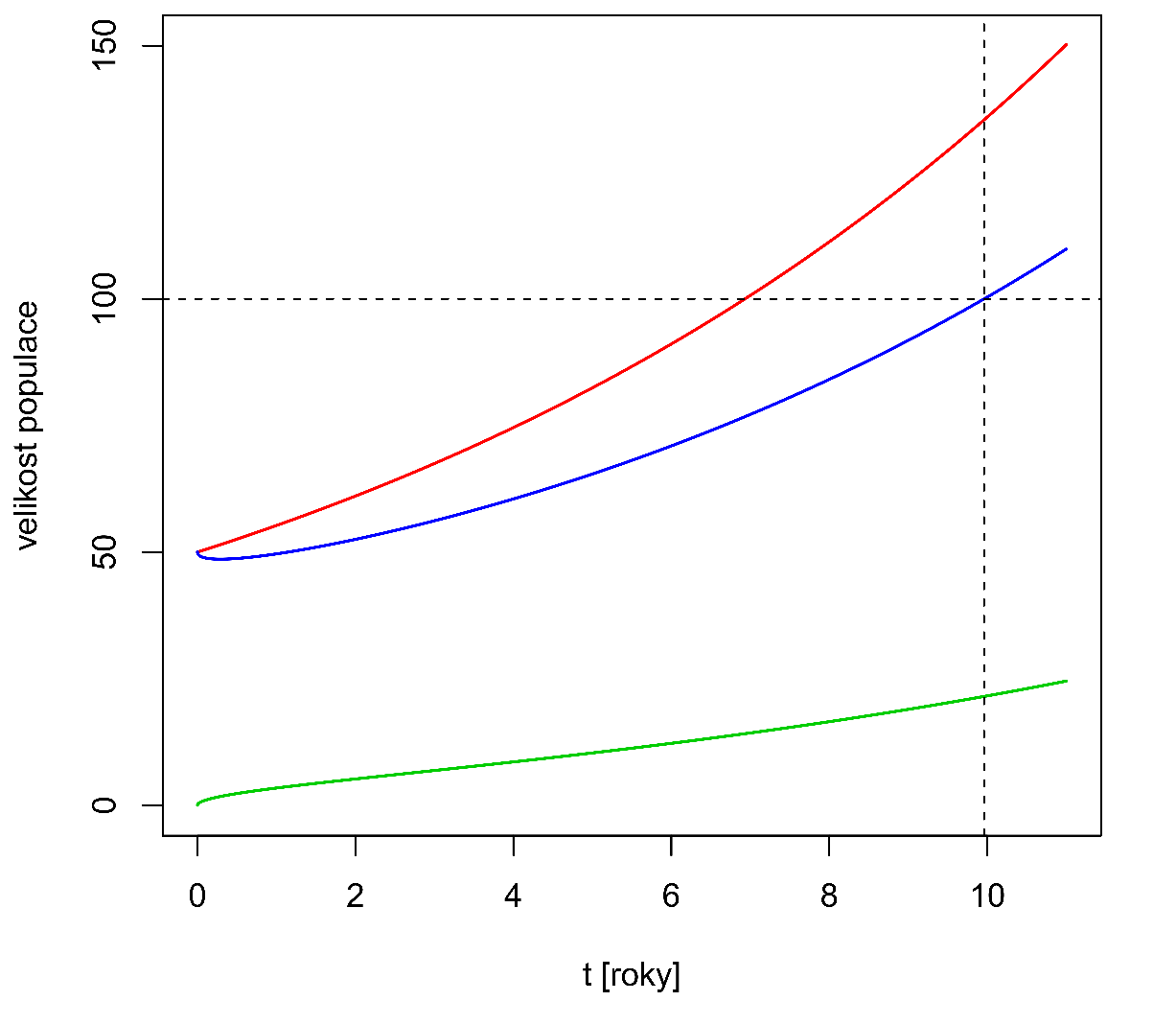Obr.3: Střední hodnota (červeně) a směrodatná odchylka (zeleně) velikosti populace v procesu vzniku a zániku s počáteční velikostí populace a paramatry /rok a /rok. Význam modré křivky je popsán v řešení úkolu 1.