Náhodná procházka s pohlcujícími stavy

Trajektorie náhodné procházky mohou obecně dosahovat nekonečných hodnot (kladných i záporných). V mnoha praktických aplikacích však takové chování neodpovídá skutečnosti, stavů je pouze konečně mnoho. Odpovídající variantu náhodné procházky si ukážeme na příkladu jednoduché hry dvou hráčů.

Příklad (Jednoduchá hra 2 hráčů)

Uvažujme hru dvou hráčů, A a B, na jejímž začátku mají hráči kapitál , resp. , korun, jde o kladná nezáporná čísla. V každém kole hráč A s pravděpodobností  vyhraje 1 korunu od hráče B, anebo prohraje 1 korunu ve prospěch hráče B s pravděpodobností . Celkový kapitál obou hráčů ve hře je konstantní, rovný .

Označme kapitál hráče A v -tém kole a položme . Kapitál hráče B analogicky označme , přičemž platí vztah , . Nechť je částka, kterou hráč A vyhraje , anebo prohraje v -tém kole hry. Náhodné veličiny , považujeme za nsr s diskrétním rozdělením pravděpodobnosti (1). Dokud mají oba hráči kladný kapitál, platí

a procesy , jsou jednoduchými náhodnými procházkami.

Hra trvá tak dlouho, dokud některý z hráčů není zruinován (nedosáhne nulového kapitálu), tzn. dokud , . Hra skončí, když (zruinování hráče A), anebo (zruinování hráče B). Procesy , tak nabývají pouze hodnot z množiny . Hodnoty 0  a jsou tzv. pohlcující (absorbční) stavy (absorbing barriers), pokud jich proces dosáhne, skončí.

Pravděpodobnost absorpce (zruinování hráče)

Hráče A zajímá, jaká je pravděpodobnost, že prohraje, tzn. že proces dospěje do pohlcujícího stavu 0. Výpočet této pravděpodobnosti je znám jako gambler's ruin problem. Označme pravděpodobnost zruinování hráče A (v kterémkoliv kroku) symbolem

(11)

Zřejmě platí a , v prvním případě je hráč A zruinován již na počátku, ve druhém případě je na počátku zruinován hráč B (a A vyhrál). Pokud ani jeden z těchto případů nenastal, proběhne alespoň jedno kolo hry. V prvním kole hráč A buď vyhraje s pravděpodobností a bude mít korun, anebo prohraje s pravděpodobností a bude mít korun. Tyto dva jevy jsou neslučitelné a můžeme tedy psát

(12)

Označíme

(13)

a substitucí převedeme (12) na systém rovnic ve tvaru

(14)

Využijeme platnosti , postupně dosazujeme z levých do pravých stran systému rovnic (14) a následně rovnice postupně sčítáme (první; první a druhou; první, druhou a třetí; atd.), čímž obdržíme vztah

(15)

V poslední rovnici dosadíme a vyjádříme z ní ,

(16)

které následně dosadíme do (15) a dostaneme

(17)

Výpočtem sum v čitateli a jmenovateli (pro se jedná o geometrické posloupnosti) obdržíme hledané pravděpodobnosti zruinování hráče A,

(18)

Grafy funkcí (18) pro několik různých pravděpodobností jsou zobrazeny na Obr.3. Vidíme, že se vždy jedná o klesající funkci, pro je navíc konkávní, pro je konvexní.

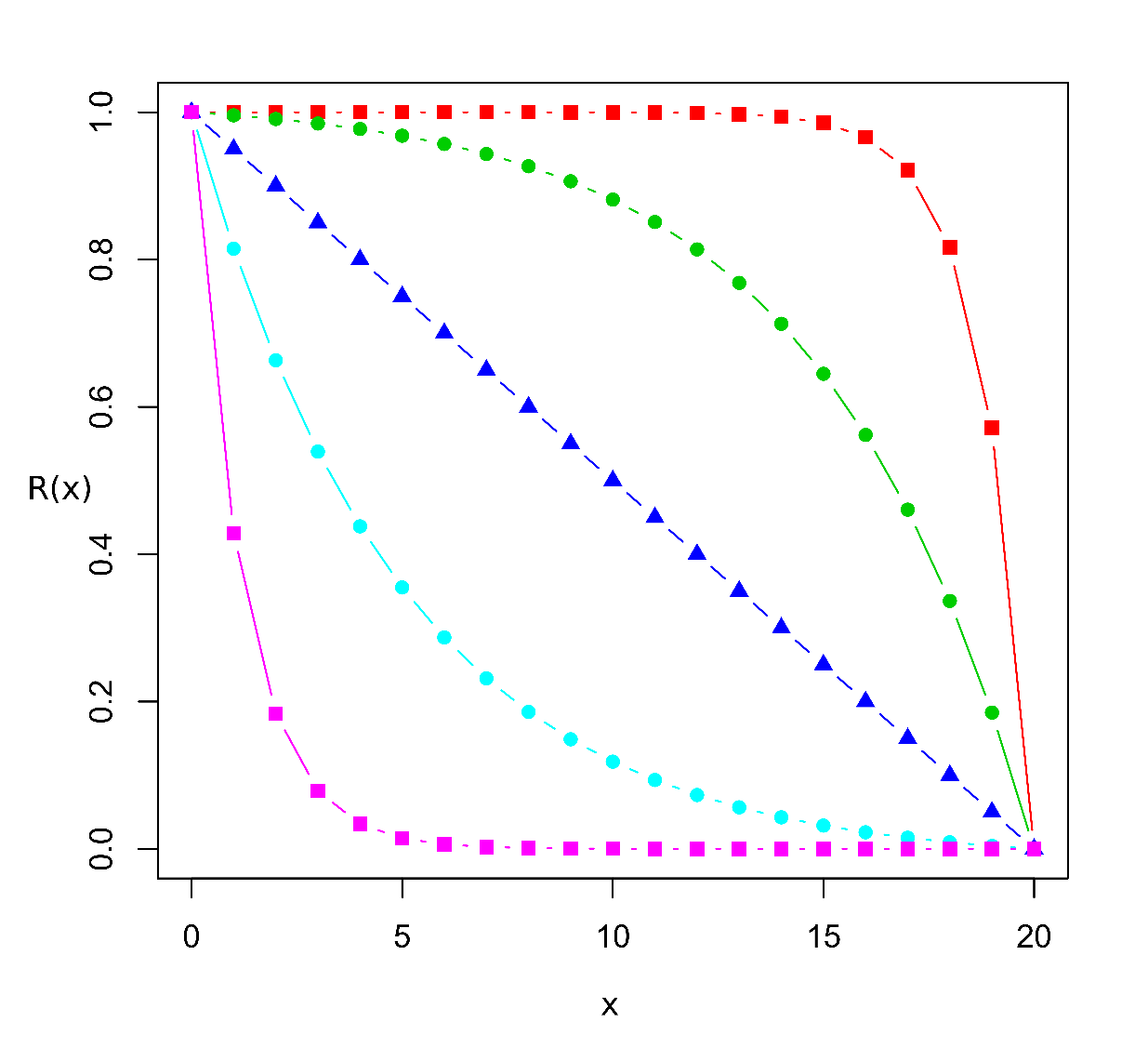Obr.3:Pravděpodobnost dosažení pohlcujícího stavu 0 (zruinování) hráčem A), , v závislosti na počátečním kapitálu . Celkový kapitál ve hře je  c = 20. Jednotlivé průběhy odpovídají pravděpodobnostem p =  0,3; 0,45; 0,5; 0,55; 0,7 (v pořadí z pravého horního do levého dolního rohu, červená; zelená; tmavě modrá; světle modrá; fialová).

Analogicky hráče B zajímá, s jakou pravděpodobností bude on zruinován. Průběh hry je z pohledu obou hráčů opačný. Pravděpodobnost zruinování hráče B, , lze spočítat pomocí (18), kde místo dosazujeme (záměna počátečního kapitálu), a místo píšeme (záměna pravděpodobností výhry v každém kole), tzn. místo máme . Takto po úpravě obdržíme 

(19)

Porovnáním (18) a (19) zjistíme, že vždy platí

(20)

tedy s pravděpodobností jedna je některý z hráčů vždy zruinován. Co když bude průběh hry takový, že v jednotlivých kolech budou hráči A a B donekonečna vyhrávat střídavě? Takový průběh by sice nevedl ke zruinování žádného z hráčů, výskyt takové trajektorie náhodné procházky má však nulovou pravděpodobnost.

Uvažme ještě variantu hry, kdy hráč A má na počátku kladný a konečný kapitál korun, zatímco hráč B má nekonečně velký kapitál, . To samozřejmě znamená, že i celkový kapitál ve hře je nekonečný, . Za jinak stejných podmínek hry chceme zjistit, jak se tato skutečnost projeví na pravděpodobnosti zruinování hráče A. Spočítáme limitu v (18) a obdržíme

(21)

tedy šance na nezruinování je pouze za podmínky . Zdůrazněme především skutečnost, že zruinování hráče A je jisté i v případě, že jednotlivá kola hry jsou spravedlivá, tedy . Tomu by odpovídala na. situace, kdy hráčem B je kasino, v němž hráč A s několikanásobně menším kapitálem v porovnání s kasinem hraje hru, která je z pohledu pravděpodobnosti férová. (Realita je samozřejmě ještě nepříznivější: .) Pokud hráč nepřestane hrát, s jistotou přijde o vše.

Doba do absorpce (do zruinování hráče)
Spočítáme střední hodnotu doby do absorpce náhodné procházky. Označme

(22)

počet kroků, než náhodná procházka dospěje do některého z pohlcujících stavů, tedy do stavu nebo . Pro střední hodnotu počtu kroků do absorpce

(23)

zřejmě platí

(24)

v prvním případě je totiž již na počátku zruinován hráč A, ve druhém případě hráč B. Pokud ani jeden z těchto případů nenastal, proběhne alespoň jedno kolo hry. V prvním kole hráč A buď vyhraje s pravděpodobností , anebo prohraje s pravděpodobností . Podle vzorce úplné pravděpodobnosti aplikovaného na podmíněné střední hodnoty lze psát

což upravíme na tvar

(25)

Systém rovnic (25) s podmínkami (24) lze vyřešit stejným způsobem jako odvození pravděpodobnosti zruinování. Uvedeme proto jen výsledek

(26)

Grafy průběhů středních hodnot (26) pro několik různých pravděpodobností jsou vykresleny v Obr.4.

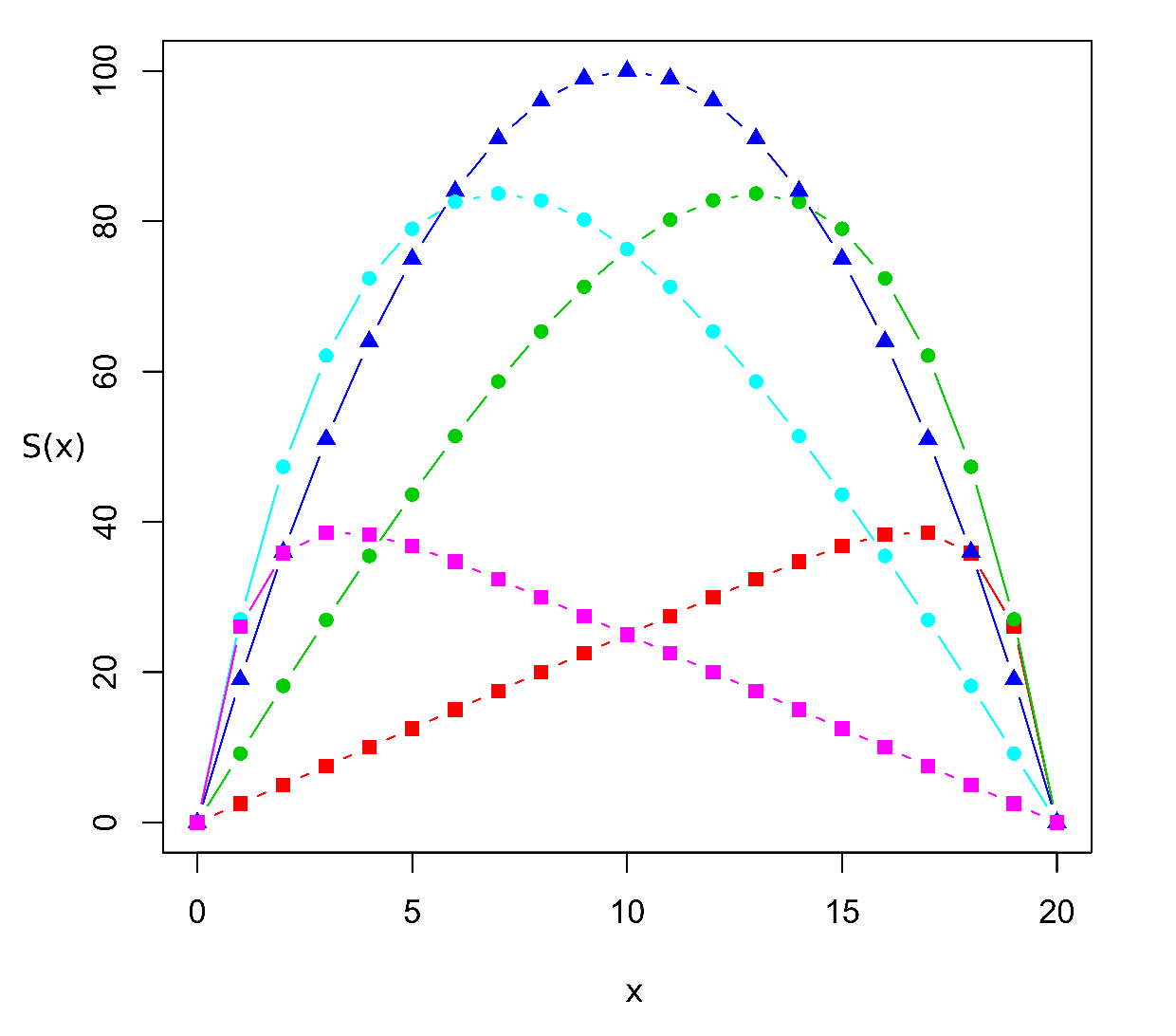Obr. 4: Střední hodnota doby do dosažení pohlcujícího stavu 0 nebo c (zruinování některého z hráčů), , v závislosti na počátečním kapitálu hráče A, . Celkový kapitál ve hře je c = 20. Jednotlivé průběhy odpovídají pravděpodobnostem p = 0,3; 0,45; 0,5; 0,55; 0,7 (v pořadí barev červená; zelená; tmavě modrá; světle modrá; fialová, stejně jako v Obr.3).

Maximální střední počet kroků do dosažení pohlcujícího stavu je rovný , a to při spravedlivé hře, , a při symetrickém rozdělení počátečního kapitálu sudé hodnoty, . Všimněme si, že na celkovém kapitálu ve hře, , závisí kvadraticky. Např. při 1,000 je maximální očekávaný počet kroků do absorpce rovný 250,000.

Na závěr ještě spočítáme střední dobu do absorpce při . Limitním přechodem v (26) obdržíme

(27)

což je ve shodě s (21).