Statistické vlastnosti intervalů mezi událostmi

Dále prozkoumáme statistické vlastnosti intervalů mezi událostmi v Poissonově procesu. Označme náhodnou veličinu udávající dobu od začátku pozorování do výskytu první události. Zvolme pevné číslo a počítejme pravděpodobnost, že první událost nastane později než v čase . Tentýž jev lze ekvivalentně vyjádřit jako , tzn. že až do času nepřišla žádná událost. Využijeme odvozené Poissonovo rozdělení a dostáváme:

(5)

Spočítali jsme vlastně funkci přežití, , náhodné veličiny . Nyní již lehce dopočítáme distribuční funkci a následně pomocí derivování i hustotu pravděpodobnosti :

	(6)
	(7)

Výsledné tvary porovnejte s (Zákon malých čísel 9) a (Zákon malých čísel 10). Vidíme, že náhodná veličina má exponenciální rozdělení pravděpodobnosti s parametrem .

Protože výskyty událostí v kterékoliv části Poissonova procesu jsou nezávislé na předchozích částech procesu, okamžik začátku měření intervalu délky lze vyjádřit v několika různých variantách, avšak se stejnými statistickými vlastnostmi:

• je doba od počátku (čas 0) do příchodu první události;
• je doba od jakéhokoliv pevně zvoleného okamžiku do příchodu první následující události;
• je doba od okamžiku kterékoliv události do příchodu první následující události, tedy mezi dvěma po sobě následujícími událostmi, tzv. interarrival time.

Označme dobu od počátku sledování do první události, délku intervalu mezi první a druhou událostí, atd., obecně délku intervalu mezi -ní a -tou událostí. Konkrétně, tyto náhodné veličiny mají exponenciální rozdělení s hustotou (Zákon malých čísel 9). Tato vlastnost je velmi důležitým znakem Poissonova procesu. V některých textech je Poissonův proces touto vlastností definován. Říkáme, že náhodné veličiny jsou vzájemně stochasticky nezávislé a stejně rozdělené. Budeme pro tento pojem užívat zkratku nsr (v angličtině se užívá zkratky
iid = independent, identically distributed) Na závěr odvodíme rozdělení pravděpodobnosti času do -té události pro   Označme takovou náhodnou veličinu , zřejmě pak platí vztah . Chceme odvodit hustotu pravděpodobnosti náhodné veličiny . Ta je, dle definice hustoty pravděpodobnosti a určitého integrálu, dána limitním podílem

Podle vlastnosti (iii) Poissonova procesu jev v čitateli nastane, právě když bude zaznamenáno událostí v intetrvalu a právě jedna událost v intervalu . Pravděpodobnost v čitateli je tedy rovna

První pravděpodobnost je rovna podle (4), druhá pravděpodobnost je určena vlastností (ii). Dostáváme tak

(8)

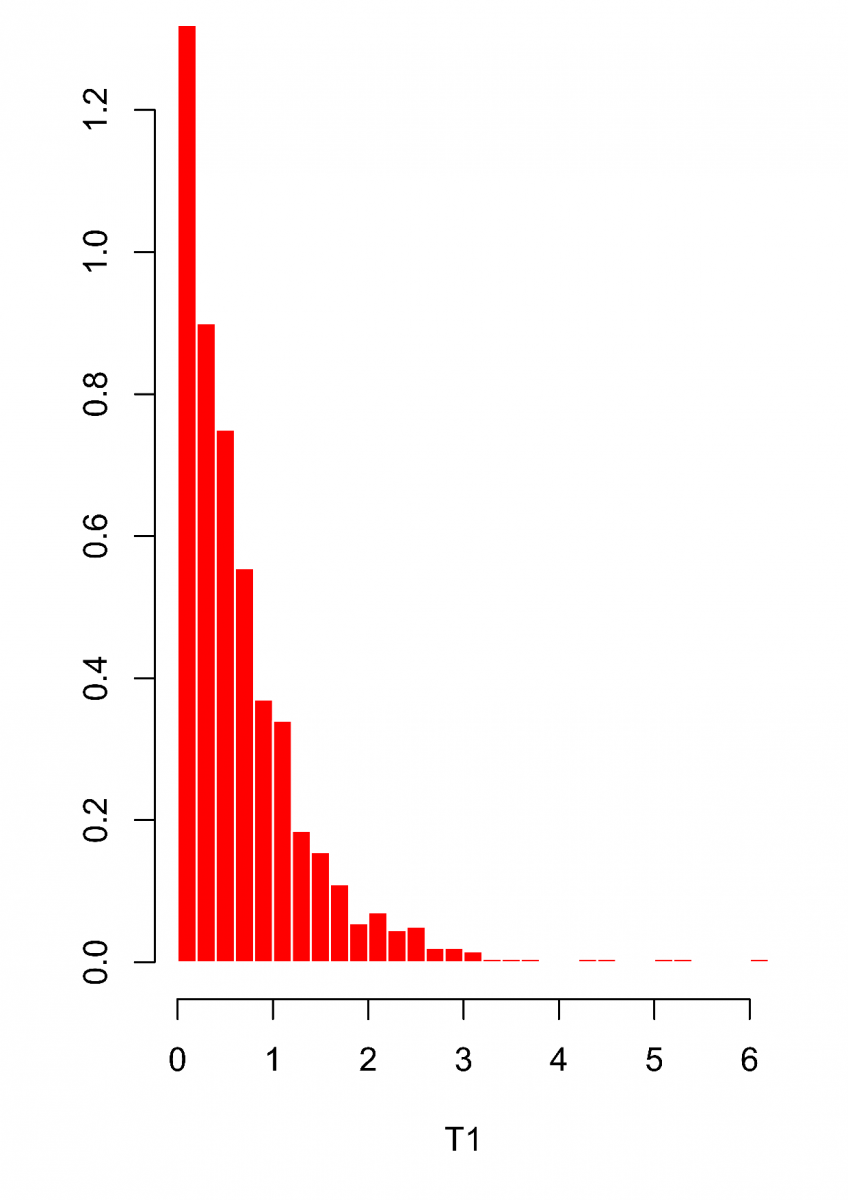
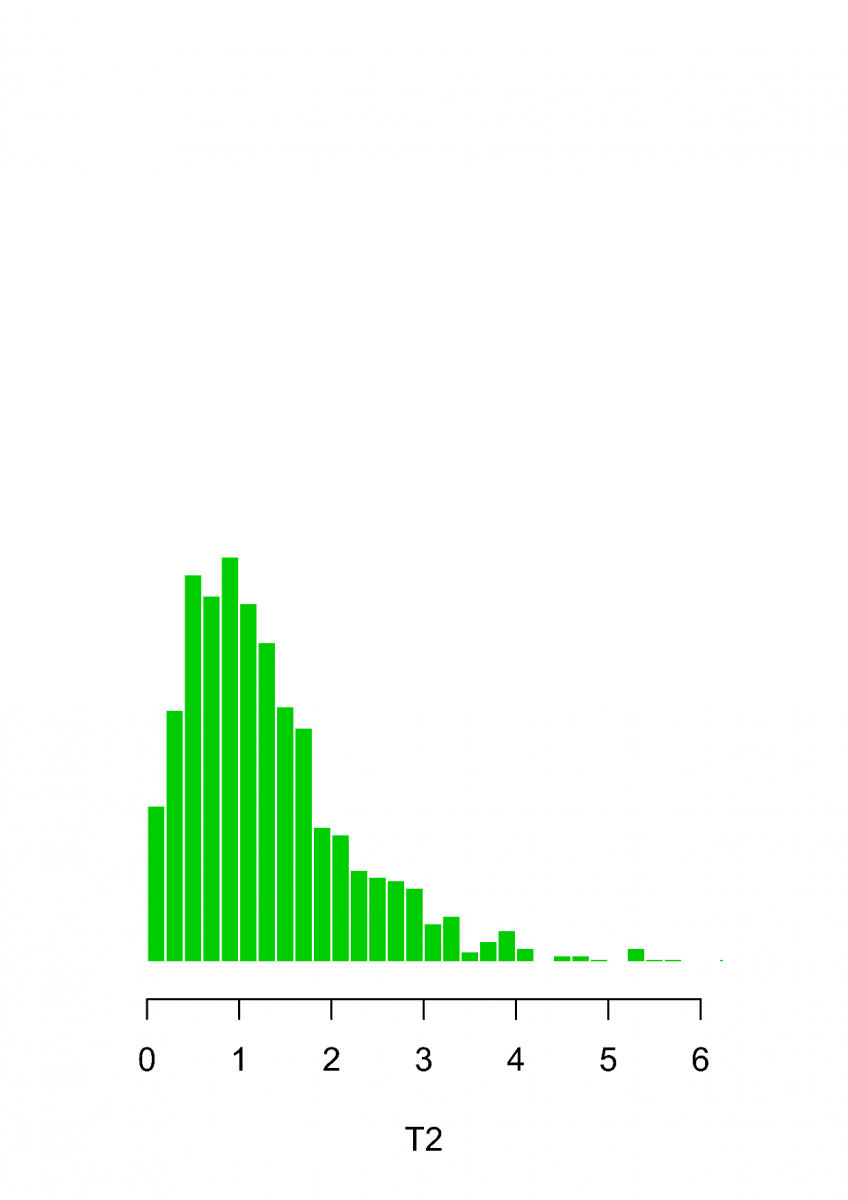
Porovnáním výsledné hustoty s (Zákon malých čísel 11) vidíme, že doba do -té události má gama (Erlangovo) rozdělení s parametrem . Histogramy délek intervalů mezi dvěma, třemi a čtyřmi po sobě jdoucími událostmi v Poissonově procesu jsou vykresleny na Obr.2. Porovnejte je s hustotami z Obr. (Zákon malých čísel 4).

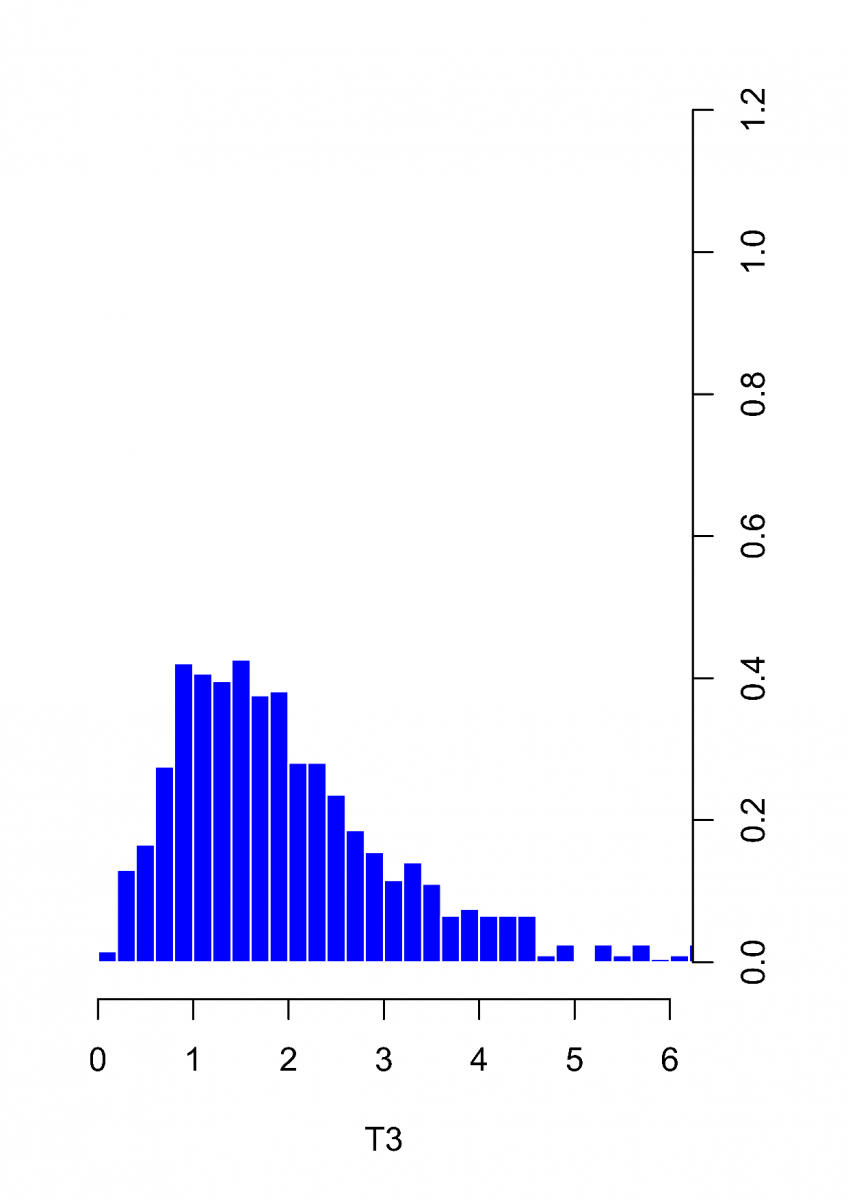Obr.2: Histogramy délek intervalů mezi dvěma (T1, červeně), třemi (T2, zeleně), resp. čtyřmi (T3, modře) po sobě následujícími událostmi ve vzorku 1000 událostí v Poissonově procesu s intenzitou .

Příklad (Spontánní nervová aktivita)
Změny elektrického potenciálu ve svalových buňkách odpovídají spontánní aktivitě v okolí nervových buněk. Časy těchto malých změn se velmi dobře popisují pomocí Poissonova procesu. Znamená to, že časy mezi dvěma takovými po sobě následujícími změnami jsou stochasticky nezávislé (tedy nekorelované) a mají exponenciální rozdělení pravděpodobnosti, což bylo potvrzeno na empirických datech.

Úkoly

1. Uvažujte dva stochasticky nezávislé Poissonovy procesy, s intenzitami . Dokažte, že náhodný proces , kde , je Poissonovým procesem s intenzitou .

Řešení

• Výpočtem ověříme vlastnosti (i), (ii), vlastnost (iii) je splněna triviálně díky vzájemné nezávislosti procesů. Počítáme pravděpodobnost, že přírůstek procesu bude rovný nule. Využijeme přitom toho, že oba dílčí procesy jsou Poissonovské:

  Přirůstek je rovný jedné, právě když jeden z procesů má přírůstek rovný jedné a druhý rovný nule,

2. Počet vozidel projíždějících v čase mýtnou branou na dálnici tvoří Poissonův proces s intenzitou . Pravděpodobnost, že vozidlo je osobní, je rovna . Dokažte, že náhodný proces, udávající počty osobních vozidel, které v čase projedou mýtnou branou je Poissonovým procesem s intenzitou .

Řešení

• Označme počty vozidel v čase   a počty osobních vozidel v čase . Na základě toho, že je Poissonův proces, ověříme vlastnosti (i), (ii) pro proces . Využijeme i toho, že charakter vozidla není závislý na čase průjezdu mýtnou branou. Přírůstek počtu osobních aut bude rovný nule, pokud za sledovanou dobu neprojede žádné auto, nebo projede jedno nákladní,

  Podobně, přírůstek počtu osobních aut bude rovný jedné, pokud projede jedno auto a to bude osobní,

  Vlastnost (iii) je splněna díky Poissonovskému charakteru počtu vozidel a jeho nezávislosti na typu vozidla.

3. Voda v nádrži je kontaminována bakterií, která se vyskytuje náhodně, průměrně v počtu jedné bakterie v 10 l vody. Když človek vypije 1 l této vody denně, jaká je pravděpodobnost, že během týdne vypije alespoň jednu bakterii?

Řešení

• Označme počet bakterií, které člověk vypije za dobu dnů. Vzhledem k náhodnému rozmístění bakterií v nádrži a zároveň nízké pravděpodobnosti výskytu více než jedné bakterie v denním objemu vypité vody považujeme za Poissonův proces. Jeho intenzita je rovna , neboť za jeden den (námi zvolená jednotka) člověk průměrně vypije bakterie (v 1 l vody). Pomocí pravděpodobnostní funkce (4) spočítáme
  
  

  Dostáváme tak pravděpodobnost .