Rozdělení pravděpodobnosti intervalů obnovy

V teto části probereme některá konkrétní, v praktickém modelování používaná rozdělení pravděpodobnosti délek intervalů obnovy, a spočítáme odpovídající rizikové funkce. Tvary rizikových funkcí jsou vykresleny na Obr.1. Exponenciální rozdělení vede na konstatní rizikovou funkci rovnou , tzn. riziko výskytu události je stále stejné, bez ohledu na délku doby bez nastání události. Gama rozdělení s vytvoří rostoucí rizikovou funkci konvergující zdola k , riziko výskytu události zde tedy roste s dobou strávenou bez nastání události, je však shora ohraničeno. Weibullovo rozdělení s vede na rostoucí a divergující rizikové funkce, pro vytváří rizikové funkce klesající asymptoticky k nule a modeluje tak situaci, kdy s rostoucím dobou bez příchodu události riziko nastání události klesá. 

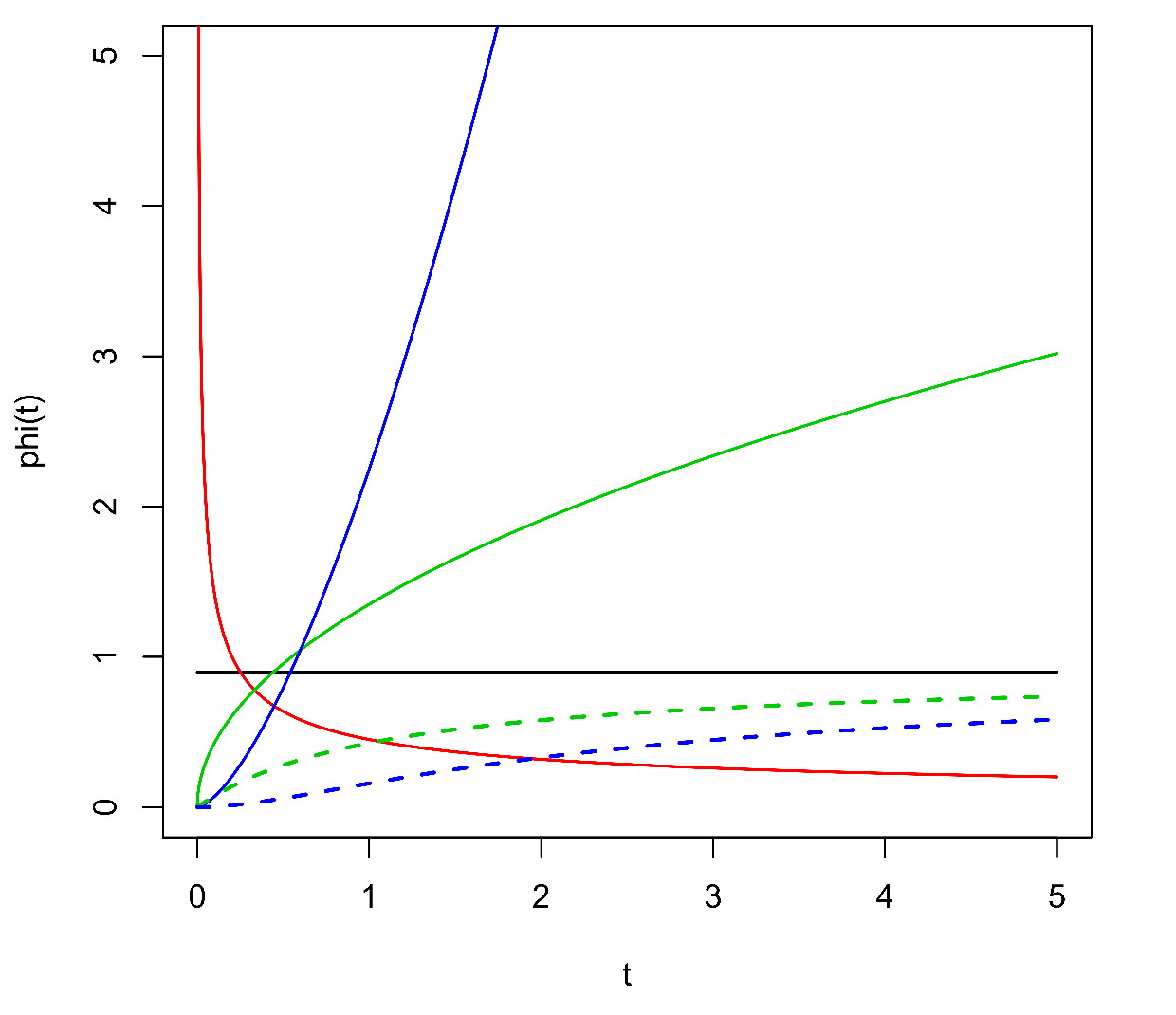Obr.1: Rizikové funkce pro různá rozdělení pravděpodobnosti. Intenzita je vždy rovna . Černě: exponenciální rozdělení . Plnou čarou: Weibullovo rozdělení: (červeně), (zeleně) a (modře). Čárkovanou čarou: gama rozdělení: (zeleně čárkovaně) a (modře čárkovaně).

Exponenciální rozdělení
Pro exponenciální rozdělení s hustotou Přibuzná rozdělení pravděpodobnosti (9) a distribuční funkcí (Zákon malých čísel 10) dostáváme funkci přežití pro . Spočítáme rizikovou funkci, 

(10)

Jak již bylo zmíněno, rizková funkce je konstantní právě pro exponenciální rozdělení intervalů obnovy, tzn. když proces obnovy je Poissonovým procesem.

Exponenciální rozdělení intervalů obnovy vede k následující zajímavé vlastnosti. Podmíněná pravděpodobnost přežití za interval délky za podmínky přežití do času je rovna 

Po dosazení dostáváme opět funkci přežití, 

Je-li tedy známo, že událost nenastala do času , je pravděpodobnost, že událost nenastane ani v následujícím intervalu_,  stejná jako je na začátku pozorování pro interval . Tato vlastnost je nazývána bezpaměťovostí, tzn. Poissonův proces je příkladem tzv. procesů bez historie, matematicky označovaných jako markovské procesy. V teorii spolehlivosti se lze setkat s následujícím sice neformálním, ale zato výstižným vyjádřením této typické vlastnosti Poissonova procesu: pracuje-li stroj do okamžiku bez poruchy, je v tomto čase stejně spolehlivý (dobrý, kvalitní), jako by byl zcela nový. Tuto vlastnost lze formulovat také tak, že v poissonovském toku událostí s rostoucí dobou čekání šance na výskyt události neroste. 

Gama rozdělení
Pro gama rozdělení pravděpodobnosti s parametry a s hustotou Přibuzná rozdělení pravděpodobnosti (11) a distribuční funkcí (Zákon malých čísel 13) spočítáme rizikovou funkci, 

(11)

Zajímavé je asymptotické chování rizikové funkce, jejíž hodnota konverguje k , tedy k hodnotě rizikové funkce exponenciálního rozdělení, 

přičemž pro je (11) rostoucí funkcí času. 

Weibullovo rozdělení
Weibullovo rozdělení pravděpodobnosti s parametry je spojitého typu s hustotou pravděpodobnosti 

(12)

Parametr je bezrozměrný, parametr má rozměr rovný k-té mocnině převrácené hodnoty jednotky času. Pro dostáváme exponenciální rozdělení, v případě je někdy nazýváno jako Rayleighovo rozdělení pravděpodobnosti. Distribuční funkce, resp.funkce přežití, tohoto rozdělení jsou rovny 

(13)

Grafy hustot a odpovídajících distribučních funkcí jsou pro některé hodnoty parametrů vykresleny na Obr. 2. 

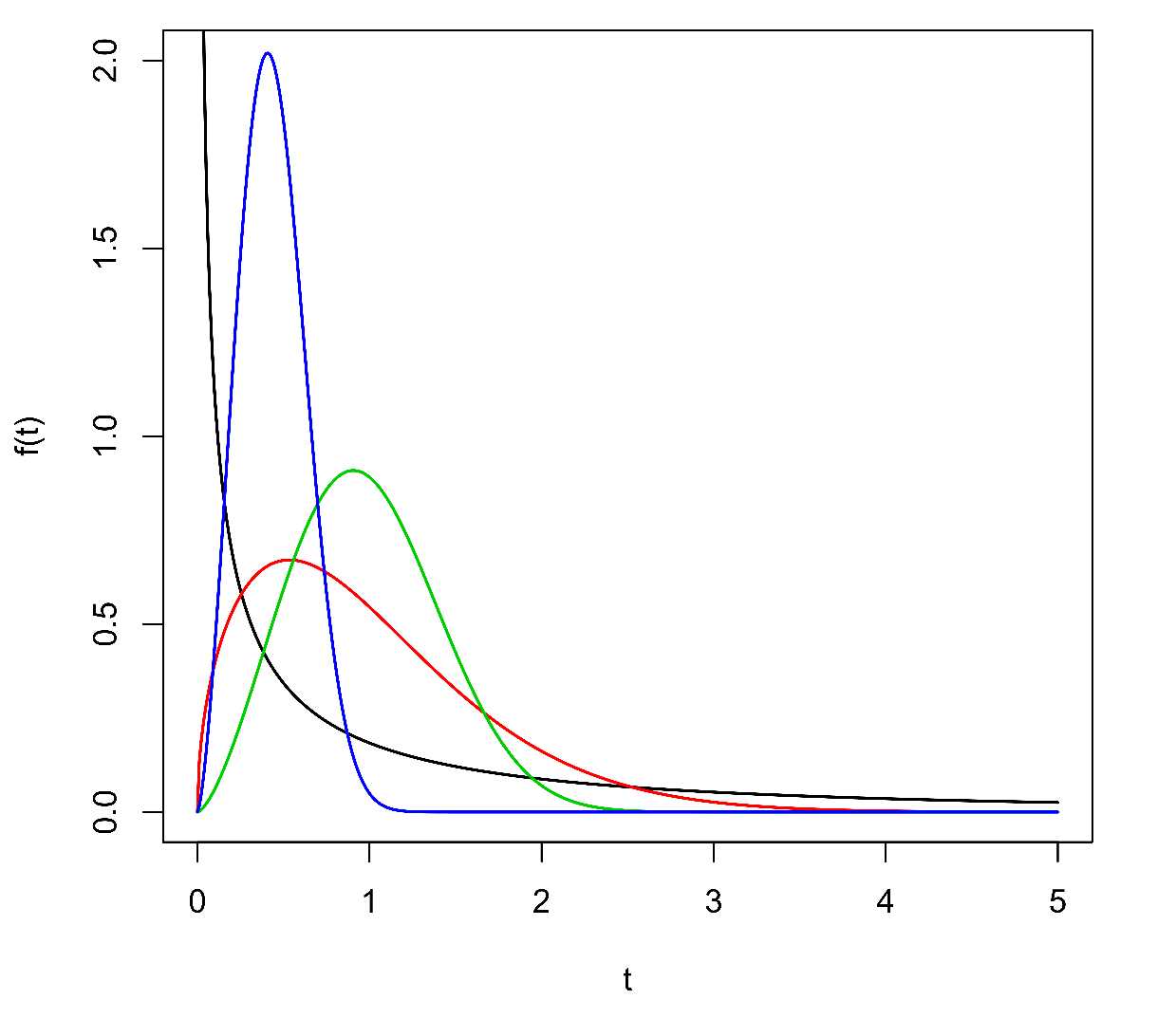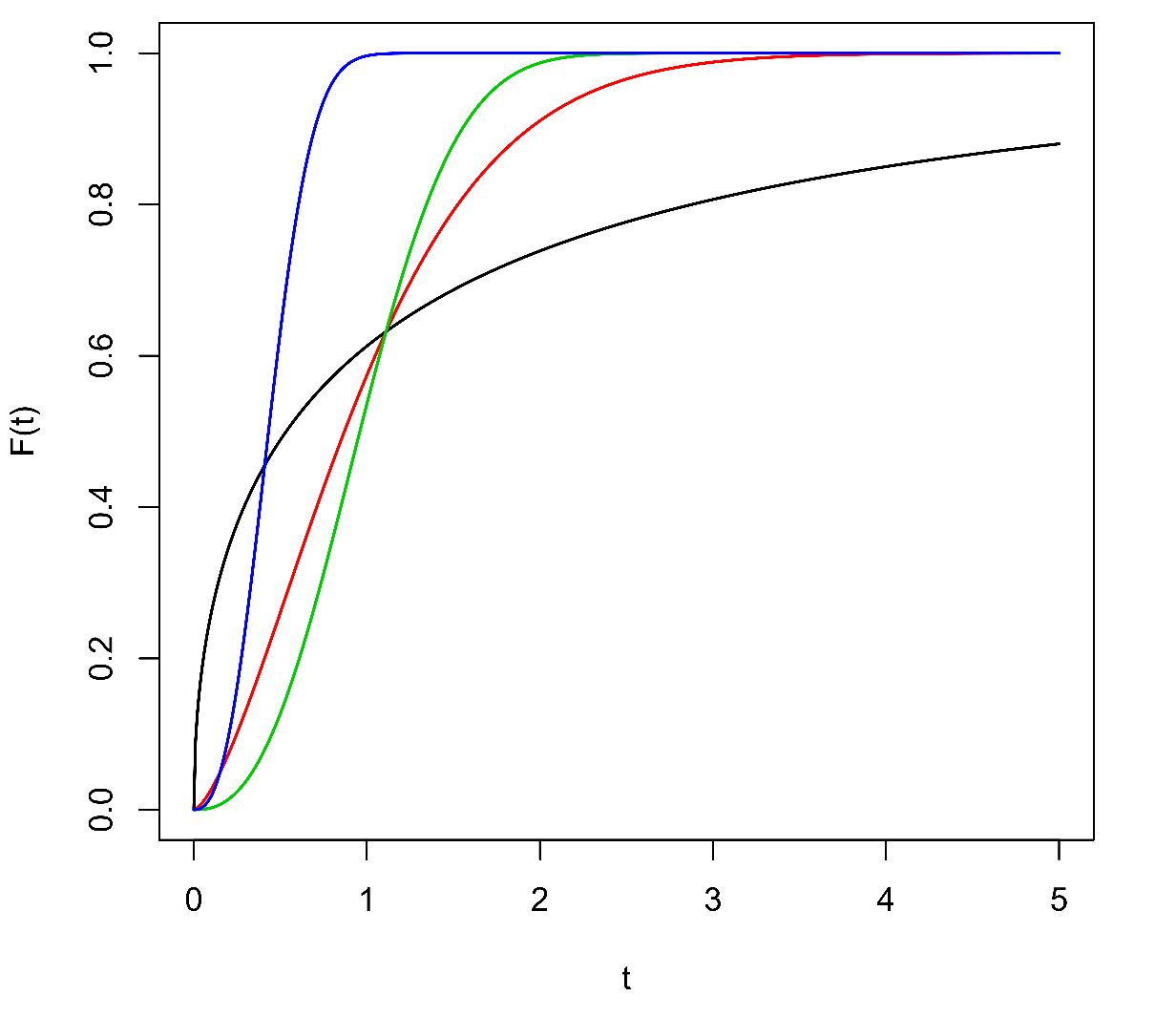Obr.2:Hustoty pravděpodobnosti a odpovídající distribuční funkce Weibullova rozdělení pravděpodobnosti. Parametry jsou:, (černě); , (červeně); , (zeleně);, (modře).

Střední hodnota a rozptyl Weibullova rozdělení jsou rovny 

	(14)
	(15)

přičemž značí gama funkci (viz (Zákon malých čísel 12)). Rizikovou funkci snadno nalezneme ve tvaru 

(16)

Ta je konstantní, rovná pro , rostoucí, divergující pro , a klesající, konvergující k 0 pro . Právě pro možnost modelovat různé tvary rizikové funkce (16) je Weibullovo rozdělení často používano v teorii spolehlivosti i v analýze přežití.