
Galtonův-Watsonův proces větvení
Z pohledu matematického formalismu je Galtonův-Watsonův proces náhodným procesem
s diskrétním časem a diskrétní množinou stavů, , s následujícími vlastnostmi:
| (i) |
|
| (ii) |
počty potomků každého jedince v každé generaci jsou nsr náhodné veličiny nabývající hodnot |
Při znalosti velikosti populace v
-té generaci lze spočítat pravděpodobnostní rozdělení počtu jedinců v následujících generacích, a to i bez znalosti velikosti populace v předchozích generacích, tzn. Galtonův-Watsonův proces je markovským procesem. Označme
náhodnou veličinu, udávající počet potomků
-tého jedince z
-té generace (potomci jsou v
-ní generaci). Z vlastnosti (ii) víme, že náhodné veličiny
jsou nsr a platí
|
|
(1) |
Pro popis počtu potomků v nulté generaci podle (i) stačí náhodná veličina . Dále je evoluce procesu popsána rekurzivním systémem rovnic
|
|
(2) |
kde vystupuje tzv. náhodný součet (náhodná suma). Ten definujeme jako nulu, pokud .
Příklad
Pro ilustraci významu zavedených náhodných veličin a
si uveďme jednu realizaci Galtonova-Watsonova procesu. Evoluce populace, která je procesem modelována, je zakreslena v Obr.1 pomocí stromového schématu. Odpovídající počty potomků,
, jednotlivých jedinců jsou uvedeny v Tab.1 . Náhodné veličiny
pro velikost populace v
-té generaci zde nabývají hodnot
|
|
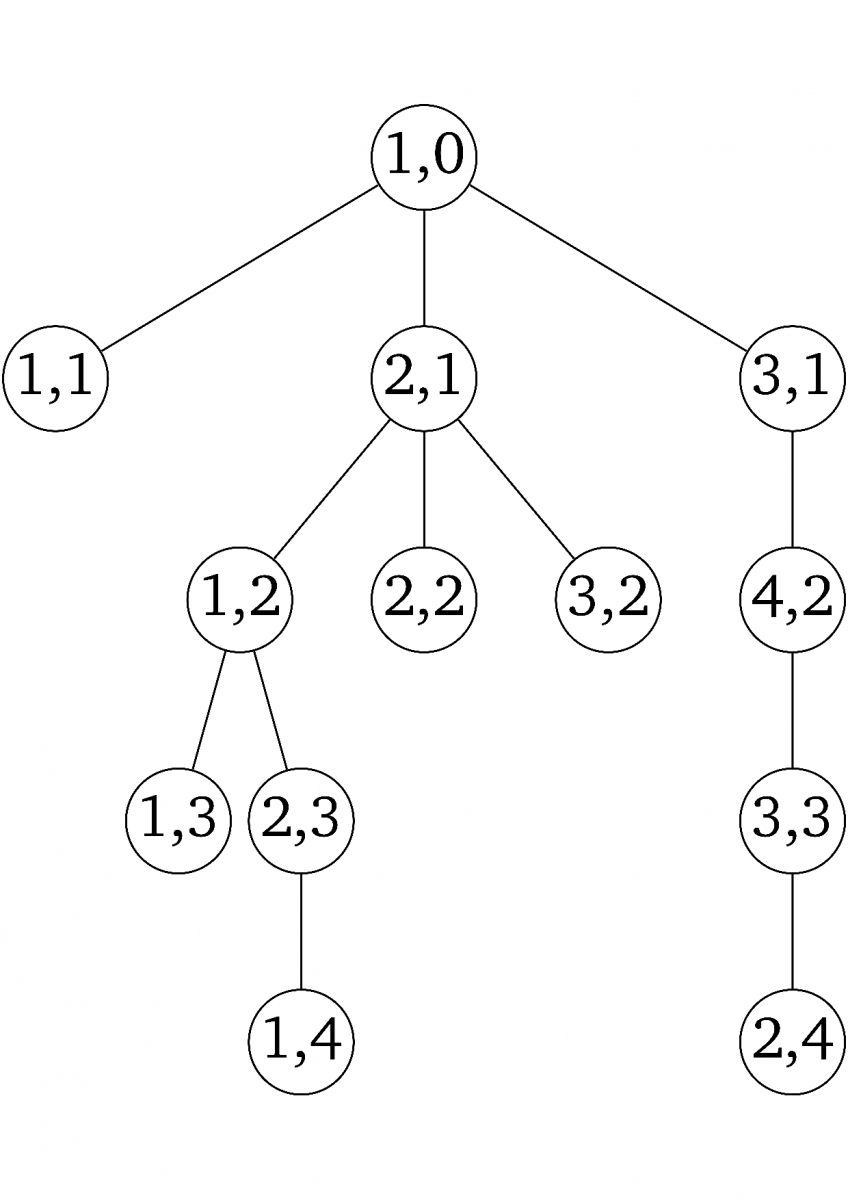 |
Obr.1: Stromové zobrazení ukazuje jednu realizaci Galtonova-Watsonova procesu větvení pro populaci, která vymře v páté generaci. Uzly značí jedince, každé patro stromu představuje jedince ve stejné generaci, mladší generace jsou umístěny níže. První číslo v uzlu vždy identifikuje jedince v generaci, druhé číslo udává pořadí příslušné generace.
|
|
Tab.1: Počty potomků jedinců v populaci z Obr.1. Neuvedené veličiny nabývají nulové hodnoty.




