Populace s parametry závislými na její velikosti

Zdroje všech populací jsou omezené, aproto žádná nemůže růst neomezeně: dříve či později narazí na horní mez svého růstu. Budeme pro jednoduchost předpokládat, že velká populace spotřebovává více zdrojů a že jejich následný nedostatek způsobí zmenšení plodností jednotlivých věkových tříd. Označme tedy a uvažujme model

(18)

Přitom funkce je nezáporná, klesající a taková, že pokud by tedy nedocházelo k uvažované vnitrodruhové konkurenci, populace by se vyvíjela podle modelu Prolog (15).

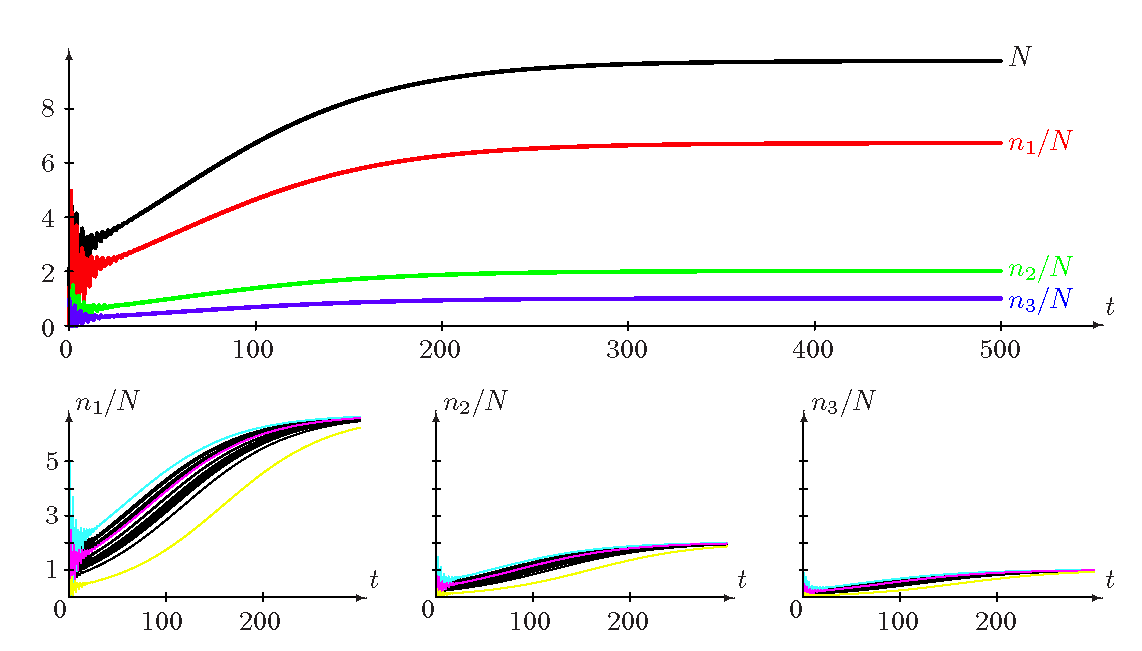
Zvolme pro určitost kde Vývoj celkové velikosti populace i jejích jednotlivých složek při použití modelu Prolog (18) s touto funkcí a s parametrem je znázorněn na obr. Prolog 7 nahoře. Vidíme, že (absolutní) velikosti jednotlivých věkových tříd se ustálí na jistých hodnotách a také celková velikost populace naroste do jisté limitní hodnoty. Tato mezní velikost populace představuje kapacitu (úživnost) prostředí pro modelovanou populaci.

Na obr. Prolog 7 dole jsou zobrazeny průběhy velikostí jednotlivých složek takto modelované populace pro různé počáteční podmínky Prolog (16). Tento výsledek naznačuje, že limitní velikosti jednotlivých věkových tříd populace nezávisí na počátečních podmínkách. Ty ovlivňují pouze rychlost konvergence.

Obr. 7. Nahoře: Vývoj populace s interní variabilitou podle modelu Prolog (18) s Dole: Vývoj velikosti jednotlivých věkových tříd populace podle první rovnosti modelu Prolog (18) s různými počátečními podmínkami Prolog (16), ty jsou v grafech rozlišeny barvami: modrá označuje první, červená druhou, žlutá třetí a černá čtvrtou podmínku, se kterou bylo provedeno 20 simulací.

Obr. 8. Vývoj populace s interní variabilitou. Populace je modelována rovnicí Prolog (18) s funkcí a různými hodnotami parametru R.

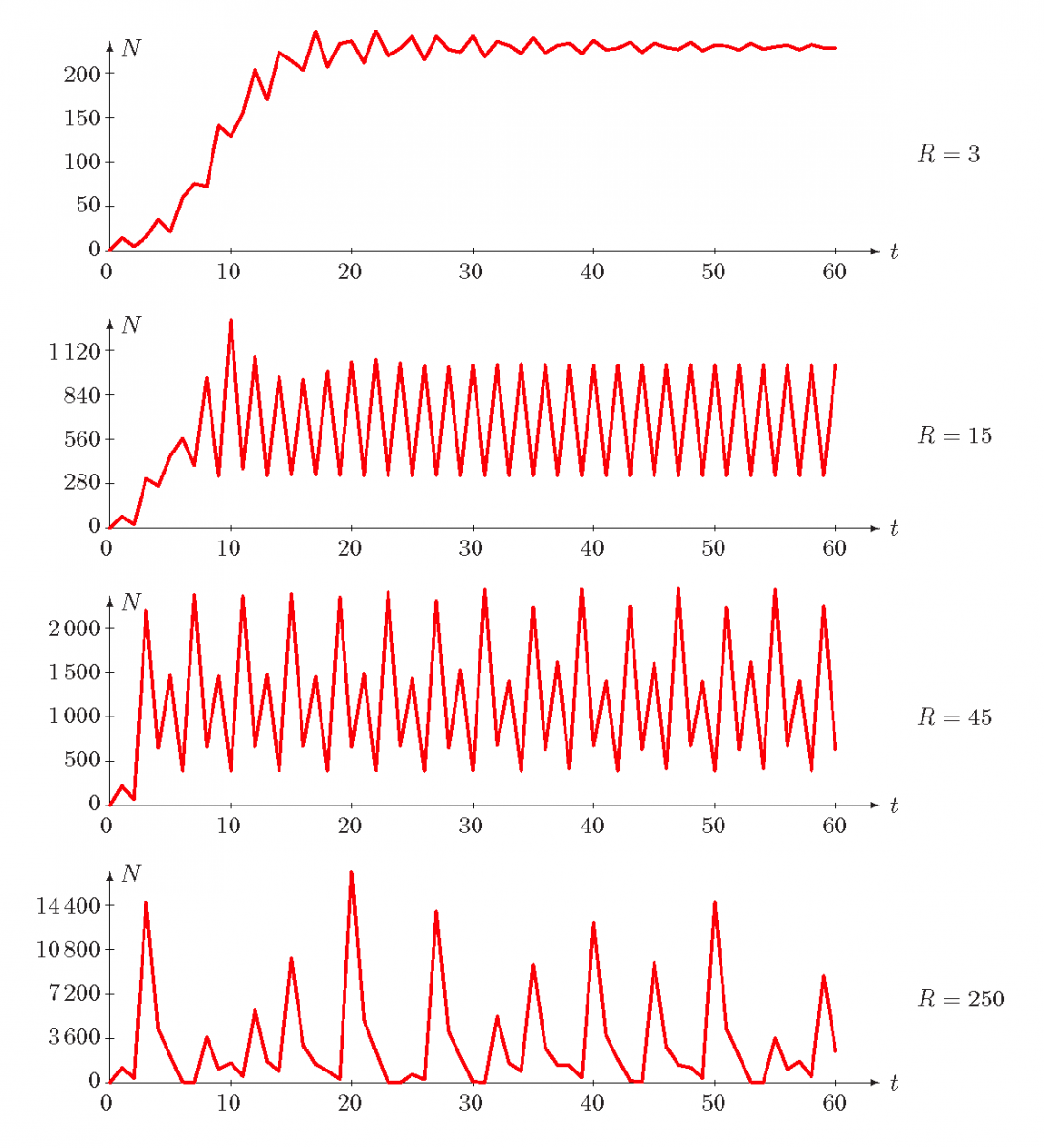
Uvažujme ještě populaci, v níž plodnost jedinců druhé věkové třídy může být větší než jednotková. Vývoj populace budeme tedy modelovat rovnostmi Prolog (18), funkce však bude dána rovností

kde Vývoj celkové velikosti populace pro různé hodnoty parametru vidíme na obr. Prolog 8. Pro se velikost populace ustálí na hodnotě kapacity prostředí a velikost populace konverguje k této limitní hodnotě s tlumenými oscilacemi. Pro a pro populace po jisté době vývoje začne kolem mezní hodnoty pravidelně oscilovat (velikost populace je od jistého času periodická, v případě je perioda rovna 2, v případě je rovna 4), pro začne kolísat a v tomto kolísání již není žádná pravidelnost vidět.