Příklad - populace strukturovaná podle plodnosti
Maticový populační model je vlastně vektorová lineární diferenční rovnice neboli systém lineárních autonomních diferenčních rovnic. Její řešení ukážeme nejprve na jednoduchém příkladu - na modelu populace rozdělené na juvenilní a plodné jedince, tj. na rovnici Prolog (9), nebo rozepsané do složek Prolog (7) a Prolog (8). Místo podmínek Prolog (6) budeme uvažovat mírně slabší podmínky
|
|
(1) |
abychom z úvah nevyloučili „klasické Fibonacciovy králíky“.
Z rovnice Prolog (7) vyjádříme
|
|
(2) |
a dosadíme do Prolog (8)
V rovnici Prolog (7) dosadíme za
a dále do ní dosadíme z předchozí rovnosti:
|
|
|
|
První složka řešení systému Prolog (9) diferenčních rovnic prvního řádu je tedy řešením lineární diferenční rovnice druhého řádu
|
|
(3) |
Její charakteristickou rovnicí je kvadratická rovnice
|
|
(4) |
která má diskriminant
|
|
|
(5) |
Vzhledem k předpokladům Modely s konstantní projekční maticí (1) je takže charakteristická rovnice Modely s konstantní projekční maticí (4) má dva reálné různé kořeny
|
|
(6) |
Kořeny a
zřejmě splňují nerovnosti
|
|
(7) |
Poznamenejme, že rovnost tj.
nastane právě tehdy, když
tedy vzhledem k Modely s konstantní projekční maticí (1) právě tehdy, když
a
Lineární diferenční rovnice druhého řádu (rekurentní formule) Modely s konstantní projekční maticí (3) má obecné řešení
Konstanty
získáme z počátečních podmínek. Předpokládejme, že známe počáteční hodnoty
a
Velikost složek populace nemůže být záporná a celková velikost existující populace je kladná, platí
|
|
(8) |
Z rovnosti Modely s konstantní projekční maticí (2) dostaneme Známe tedy hodnoty
a
které musí splňovat rovnosti
Řešením tohoto systému rovnic pro neznámé parametry
je
takže
Druhou složku řešení systému Prolog (9) dostaneme dosazením vypočítané první složky do rovnosti Modely s konstantní projekční maticí (2):
Řešení systému Prolog (9) tedy je
|
|
|
kde a
jsou dány rovnostmi Modely s konstantní projekční maticí (5) a Modely s konstantní projekční maticí (6). Řešení systému Prolog (9) lze také stručně zapsat ve tvaru
|
|
(9) |
kde
|
|
|
|
|
|
Přímým výpočtem můžeme ověřit, že
jsou vlastními hodnotami matice
a vektory
jsou příslušné vlastní vektory. Z rovností Modely s konstantní projekční maticí (5), Modely s konstantní projekční maticí (6) a nerovností Modely s konstantní projekční maticí (1) dostaneme
Z těchto nerovností plyne
|
|
(10) |
Ze druhé z nich spolu s nerovnostmi Modely s konstantní projekční maticí (7) a Modely s konstantní projekční maticí (8) plyne
|
|
(11) |
Z vyjádření řešení Modely s konstantní projekční maticí (9) dostaneme
|
|
(12) |
Označme dále
poměr velikostí složek populace (daných rovností Modely s konstantní projekční maticí (9)) v čase Nerovnosti Modely s konstantní projekční maticí (7), Modely s konstantní projekční maticí (10) a Modely s konstantní projekční maticí (11) ukazují, že veličina
je definována korektně.
Nechť tj.
nebo
Podle nerovností Modely s konstantní projekční maticí (7) je
a tedy
V tomto případě je
|
|
13 |
tj. funkce a
jsou asymptoticky ekvivalentní, a
Pokud navíc což podle Modely s konstantní projekční maticí (5) a Modely s konstantní projekční maticí (6) nastane právě tehdy, když
pak
|
|
(14) |
a
Je-li , tj.
podle Modely s konstantní projekční maticí (7), pak
takže
Dále
Pro velikost vektoru na pravé straně této rovnosti vzhledem k Modely s konstantní projekční maticí (10) platí
|
|
(15) |
Velikost vektoru řešení rovnice Prolog (9) tedy v každém případě podle rovností Modely s konstantní projekční maticí (13), Modely s konstantní projekční maticí (14) a Modely s konstantní projekční maticí (15) splňuje asymptotickou rovnost
|
|
(16) |
velikost populace se „po dostatečně dlouhém vývoji chová jako geometrická posloupnost s kvocientem “.
Dosud provedené výpočty můžeme shrnout:
- Matice
v rovnici Prolog (9) má dvě reálné různé vlastní hodnoty
takové, že
- Vlastní vektor
příslušný k vlastní hodnotě
má obě složky kladné.
- Řešení rovnice Prolog (9) je dáno formulí Modely s konstantní projekční maticí (9). Přitom
jsou vlastní vektory příslušné k vlastním hodnotám
a
závisí na počátečních podmínkách
- Řešení
rovnice Prolog (9) je asymptoticky ekvivalentní s geometrickou posloupností s kvocientem
-
Pokud
pak poměr složek vektoru řešení
Pokud $, pak poměr složek vektoru řešení
Kladná vlastní hodnota matice
(dominantní vlastní hodnota) tedy představuje růstový koeficient populace. V případě populace iteroparní (
) nebo populace se zpožděným dospíváním (
) se poměr velikostí jednotlivých tříd v průběhu vývoje ustálí; složky normovaného vlastního vektoru příslušného k dominantní vlastní hodnotě, tj. vektoru
představují relativní zastoupení jednotlivých tříd, tedy stabilizovanou strukturu populace.
 |
|
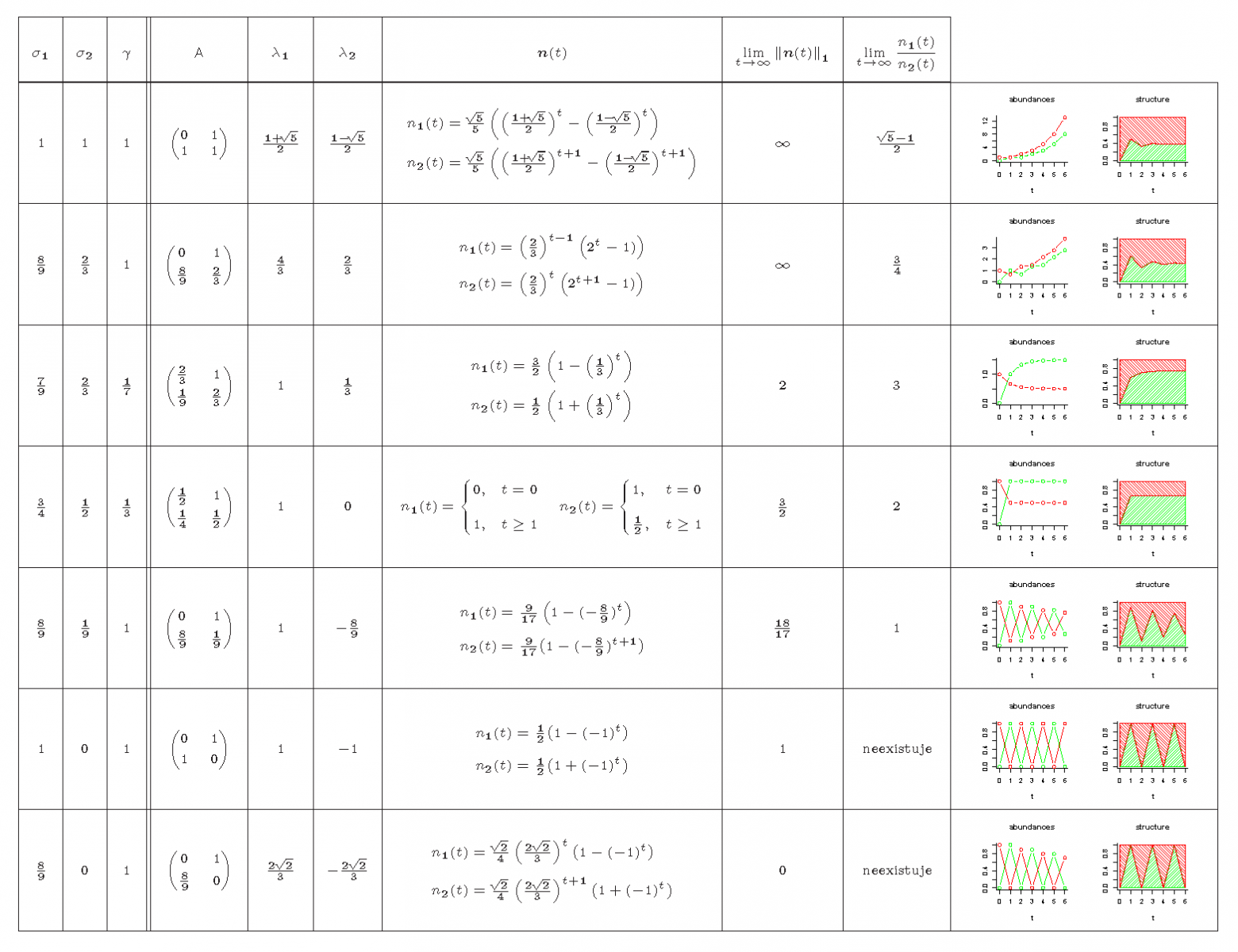Tab. 1. Speciální případy modelu Prolog (9) a jejich řešení. Ve všech modelech jsou počáteční podmínky n1(0)=0, n2(0)=1 a plodnost
|
Výsledky lze také ilustrovat několika konkrétními případy. Za jednotku času (délku projekčního intervalu) zvolíme dobu potřebnou k „vyprodukování“ jednoho potomka. Bude tedy Za počáteční hodnoty zvolíme
tedy stejně jako v případě Fibonacciových králíků začínáme s jedním plodným párem. Platí tedy
a řešení je tvaru
kde
Výsledky pro několik zvolených hodnot parametrů jsou shrnuty v tabulce Modely s konstantní projekční maticí 1. Vidíme, že celková velikost populace může neomezeně růst, klesat k nule (populace vymírá), konvergovat k nějaké hodnotě, případně této hodnoty bezprostředně dosáhnout. V případě, že populace není semelparní s bezprostředním dospíváním, struktura populace (relativní zastoupení jednotlivých složek) konverguje k nějaké hodnotě; k této hodnotě struktura konverguje monotonně nebo s tlumenými oscilacemi, případně jí dosáhne hned v prvním časovém kroku.
