Log-lineární modely

Zkusme se na kontingenční tabulky dívat pohledem zobecněných lineárních modelů. V předchozím případě hypotéza nezávislosti vede k multiplikativnímu modelu, který logaritmováním lze převést na model lineární a odtud pramení všeobecně zažité pojmenování log-lineární modely.

Nyní pro předchozí model hledejme odpovídající GLM model:

Pro model s celkovou dodatečnou podmínkou lze hypotézu o nezávislosti dvou faktorů definovat takto

V GLM s log-lineární linkovací funkcí máme tedy

Pokud bychom nepředpokládali nezávislost faktorů A a B, dostaneme maximální model

Vidíme, že základní i maximální modely jsou přeparametrizovány. Proto se musí upravit, například tak, že položíme

nebo

Všimněme si počtů parametrů pro jednotlivé úrovně

	obecná střední hodnota
	hlavní efekt
	hlavní efekt
	interakce prvního řádu
	celkem

Vidíme, že hypotéza nezávislosti dvou faktorů v kontingenčních tabulkách je ekvivalentní s hypotézou neexistence interakcí v analýze rozptylu (deviace), tj.

V log-lineárních modelech jsou obvykle výrazy vyšších řádů definovány jako odchylky od výrazů nižšího řádu. Tak například v základním modelu výraz reprezentuje rozdíl efektu řádku od obecné střední hodnoty Takže model je hiearchický v tom smyslu, že výrazy vyšších řádů nejsou obsaženy ve výrazech nižších řádů.

Shrňme předchozí výsledky:

V této kapitole jsme se pokusili o stručný popis modelování kontingenčních tabulek v souvislosti se zobecněnými lineárními modely. Pro podrobnější analýzu závislosti náhodných veličin pomocí kontingenčních tabulek odkazujeme čtenáře na další kapitolu.

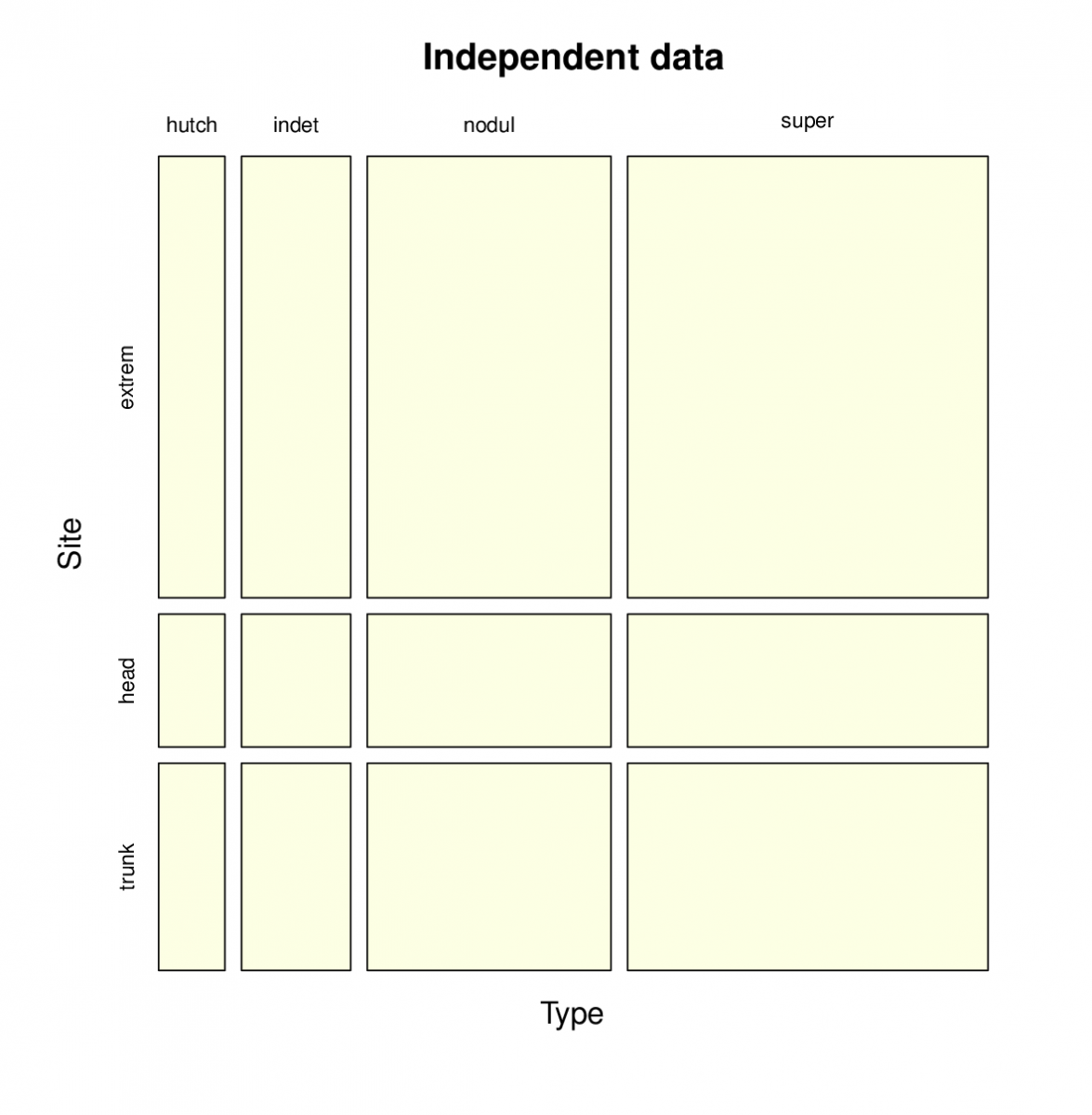
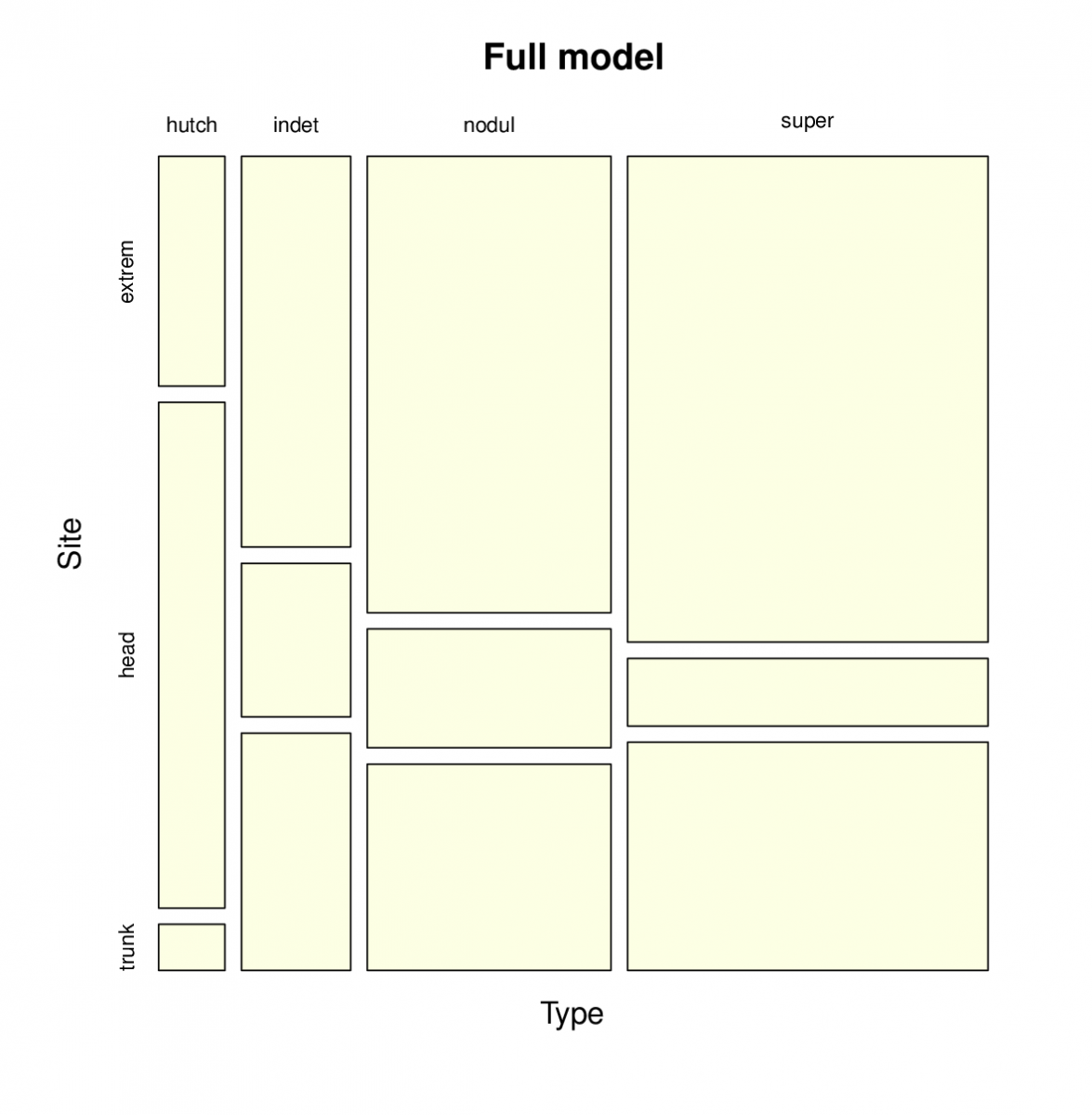
Příklad. V následující kontingenční tabulce jsou obsaženy údaje studie 400 pacientů o počtech různých typů onemocnění rakovinou kůže (Malignant Melanoma) v závislosti na části těla, kde se vyskytují.

Na hladině významnosti testujte hypotézu, zda typ rakoviny kůže závisí na části těla, kde se vyskytuje.

Řešení. Nejprve definujeme oba log-lineární modely, tj. model m1, který předpokládá nezávislost obou faktorů a model m2, který počítá i s interakcemi. Model m1 je tedy submodelem modelu m2. K testování využijeme analýzu deviace, Pearsonův test. Jeho -hodnota vychází a proto zamítáme hypotézu o nezávislosti typu rakoviny kůže na části těla, kde se vyskytuje. Výsledky obou modelů lze také znázornit pomocí mozaikového grafu. Graf pro model m1 je znázorněn na obr. Konkrétní GLM modely 11, graf pro model m2 je vykreslen na obr. Konkrétní GLM modely 12.

Obr. 11. Mozaikový graf pro model, který předpokládá nezávislost.

Obr. 12. Mozaikový graf pro model s interakcemi.