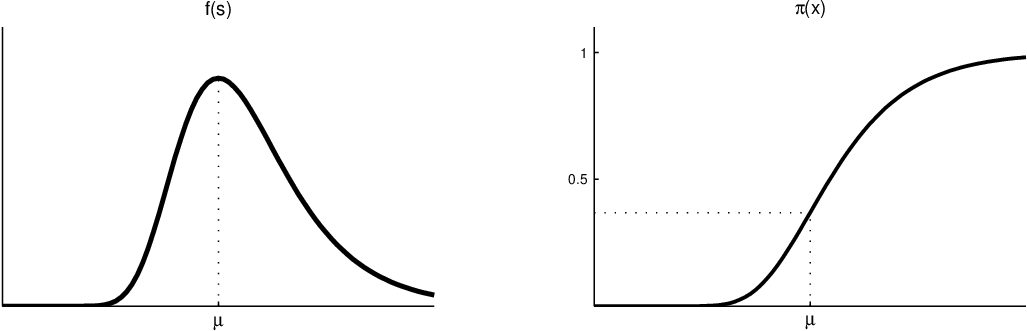
Modely dávka - odpověď

Typickým příkladem těchto modelů je vztah mezi dávkou toxické látky a odezvy (kladná-přežití, záporná-smrt) jedince  na tuto dávku. Odezvy bývají obvykle udávány jako procenta kladné odezvy (quantal responses).

Symetrické modely

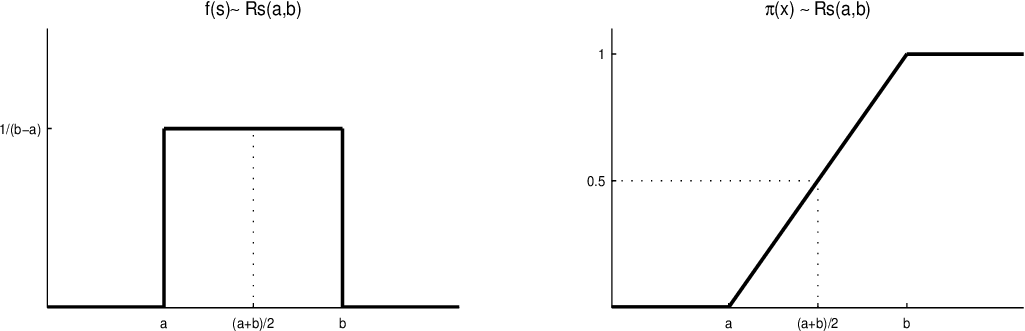
Definice 2.1. Jestliže uvažujeme toleranční distribuci jako rovnoměrně spojitou na nějakém intervalu tj

pak

a tento model je lineárním modelem

s identickou linkovací funkcí

Obr. 1. Rovnoměrné rozdělení na

V praxi tento model však nemá přílišné uplatnění.

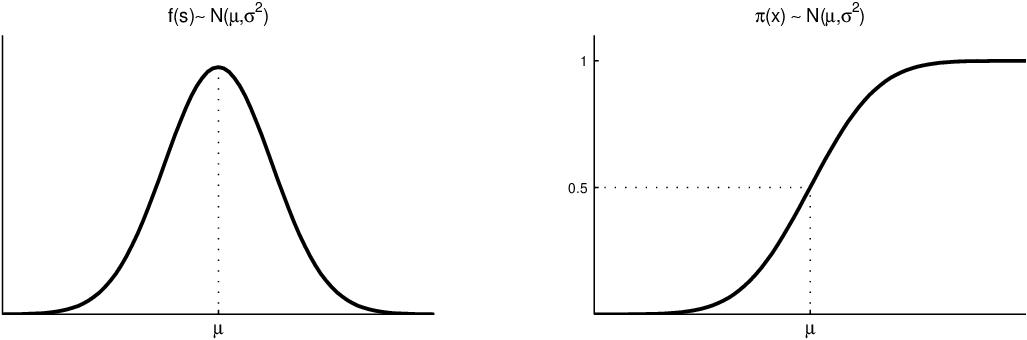
Obr. 2. Normální rozdělení

Další možností je vzít normální hustotu jako toleranční funkci. Připomeňme, že střední hodnota, medián i modus je roven parametru a rozptyl parametru

Definice 2. 2. Jestliže toleranční funkcí je normální hustota, mluvíme o probitovém modelu:

kde je distribuční funkce standardizovaného normálního rozdělení. Pak  tzv. probitovou linkovací funkcí je kvantilová funkce normálního rozdělení

Hodnota mediánu se nazývá  mediánová smrtící dávka (median lethal dose - LD50) a odpovídá dávce, při které polovina jedinců má kladnou a polovina zápornou odezvu. Probitový model má široké uplatnění v biologických a sociálních vědách.

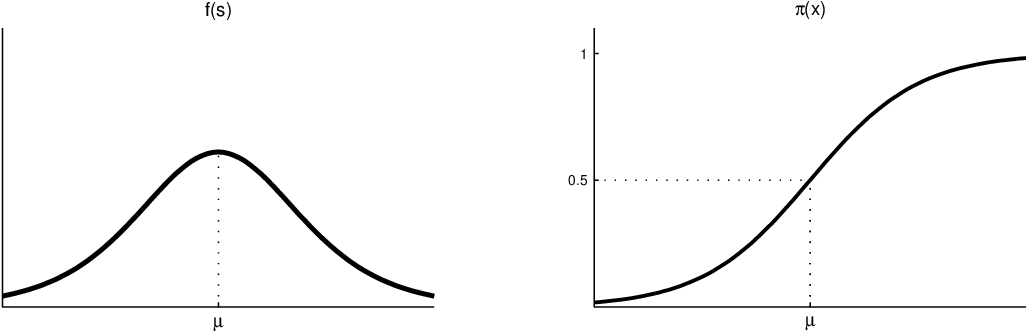
Obr. 3. Logistické rozdělení.

Definice 2.3. Logistický model je model, kde toleranční funkce je hustota logistického rozdělení (se střední hodnotou, mediánem i modusem a rozptylem )

takže

s tzv. logit linkovací funkcí

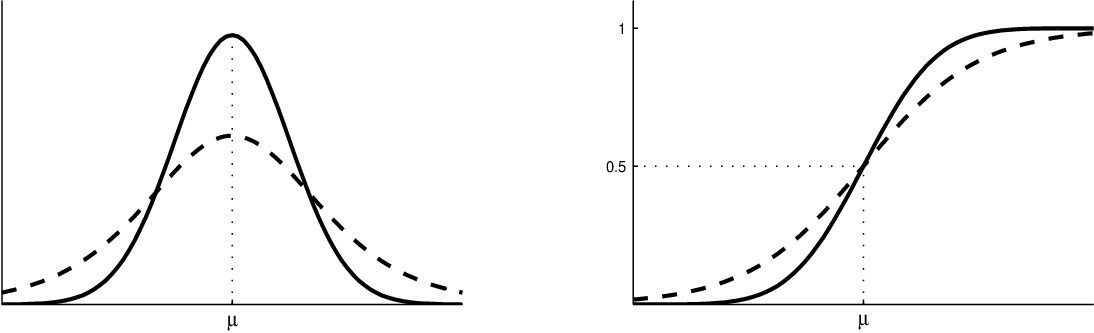
Obr. 4. Srovnání probitového a logistického (- - -) modelu při stejných parametrech a Názorně je vidět, že logistický model má větší rozptyl a těžší konce.

Asymetrické (extremální) modely

Definice 2.4. Pokud za toleranční funkci zvolíme Log-Weibullovo rozdělení (extreme-minimal-value distribution) ve tvaru

pak

s tzv. komplementární log-log linkovací funkcí

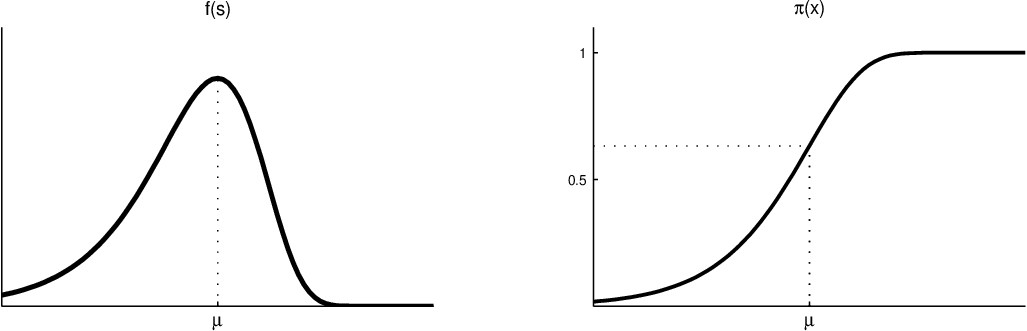
Obr. 5. Log-Weibullovo rozdělení.

Pro výše uvedené rozdělení můžeme vyjádřit jeho číselné charakteristiky:

Definice 2.5. Pokud jako toleranční funkci zvolíme zobecněné Gumbelovo rozdělení (extreme-maximal-value distribution) ve tvaru

dostaneme

s tzv. log-log linkovací funkcí

Pro výše uvedené rozdělení opět vyjádřeme jeho číselné charakteristiky:

Poznámka 2.6. Pokud náhodná veličina  má rozdělení rovnoměrně spojité na intervalu tj.

pak