Lineární regresní model

Předpokládejme, že mezi nějakými nenáhodnými veličinami  platí lineární vztah

ve kterém  jsou neznáméparametry. Informace o neznámých parametrech budeme získávat pomocí experimentu, a to tak, že opakovaně budeme měřit hodnoty veličiny při vybraných hodnotách proměnných  Při měřeních však vznikají chyby, což lze modelovat takto

kde  je náhodná chyba měření.

Opakované hodnoty sledovaných veličin budeme pro  značit  obdobně také náhodné chyby
Celkově jsme dostali model

O náhodných chybách  budeme předpokládat, že jsou

• nesystematické, což lze matematicky vyjádřit požadavkem, že   , tj.  a tedy 
• homogenní v rozptylu, tj. že   pro
• jednotlivé náhodné chyby jsou nekorelované, tj. že   pro  tj.  takže i měření jsou nekorelovaná.

Používá se následující terminologie a značení

• parametry  se nazývají regresní koeficienty,
• matice  obsahuje nenáhodné prvky  a nazývá se regresní maticí nebo maticí plánu (Design Matrix),
• popsaný model souhrnně zapíšeme jako 

Takto zavedený model budeme nazývat lineární regresní model. Dále budeme předpokládat, že   a o hodnosti matice  budeme předpokládat, že je rovna tj.   Bude-li tento přepoklad splněn, budeme říkat, že jde lineární regresní model plné hodnosti. V tom případě  jsou sloupce matice  nezávislé.

V opačném případě, by bylo možné daný sloupec matice  napsat jako lineární kombinaci ostatních sloupců, což je možné interpretovat tak, že proměnná odpovídající danému sloupci je nadbytečná, protože ji lze vyjádřit jako lineární funkci ostatních proměnných.

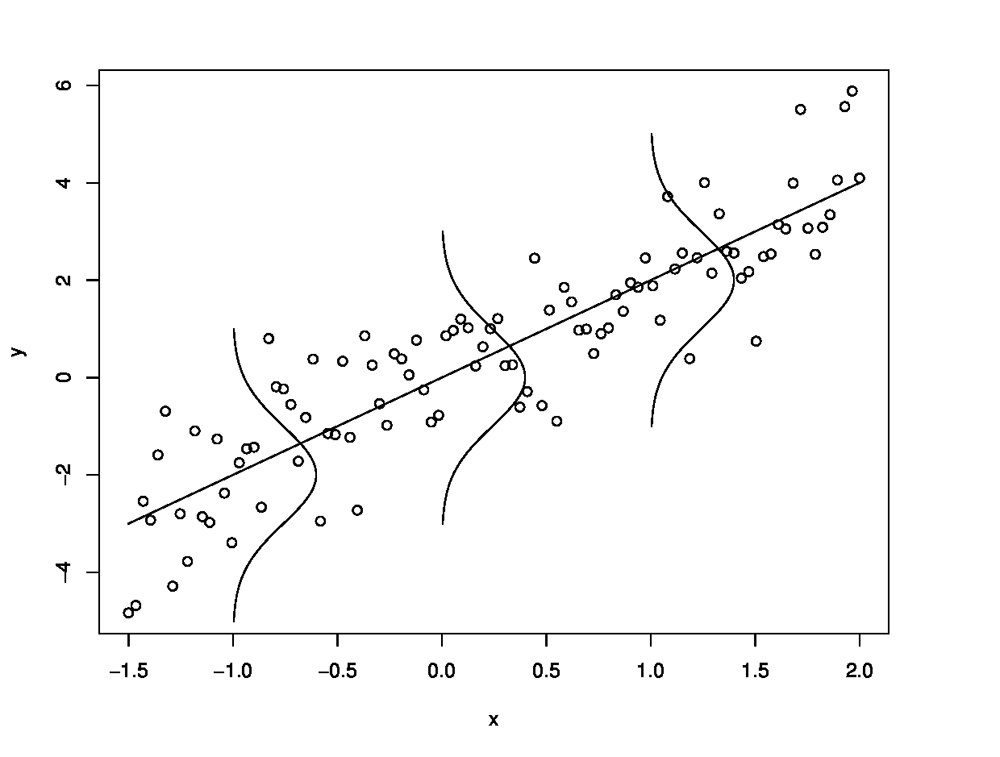
Příklad 2.1. REGRESNí PŘÍMKA V KLASICKÉM LINEÁRNÍM REGRESNÍM MODELU

Klasickým speciálním případem lineárního modelu je jednoduchá lineární regrese, kdy předpokládáme, že nezávislé náhodné veličiny  mají normální rozdělení     kde   jsou dané konstanty, které nejsou všechny stejné. Rozptyly  jsou stejné, kdežto střední hodnoty lze vyjádřit jako lineární funkci známých konstant  pomocí neznámých parametrů

V tomto případě